


Theoretische und numerische Untersuchungen zu den geodätischen Hauptaufgaben
Armin Retterath
In diesem Abschnitt werden zunächst die Begriffe Mannigfaltigkeit und Riemannscher
Raum mit ihrer differentialgeometrischen Bedeutung kurz erläutert. Außerdem
soll die Interpretation der Christoffelsymbole als Elemente des affinen Zusammenhangs
in der von einer Einbettung unabhängigen Riemannschen Geometrie herausgestellt
werden.
Wenn der Mensch den Begriff des Raumes verwendet, so verbindet er mit diesem
einen dreidimensionalen ausgedehnten Raum, welchen er mit seinen Sinnen erfassen
kann. Er kann den, seinen Sensoren zugänglichen Punkten des Anschauungsraumes,
durch Messen von Richtungen und Abständen eine gegenseitige Lage zuordnen. Es
sind nun, um die Eindeutigkeit der Zuordnungen zu gewährleisten, Vereinbarungen
über den Maßstab und den Bezugspunkt der Messungen nötig. Dies führt zu einer
Einführung von gewissen Berechnungsvorschriften, die dem Anschauungsraum eine
einfache Ordnung geben. Um Berechnungen zwischen den Raumpunkten durchführen
zu können, müssen die Punkte des Raumes einer mathematischen Beschreibung zugänglich
gemacht werden.
Betrachtet man eine Menge 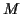 von
von 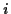 Punkten in einem n-dimensionalen
Raum
Punkten in einem n-dimensionalen
Raum 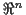 , welche im folgenden mit Mannigfaltigkeit bezeichnet
wird und einen Vektorraum
, welche im folgenden mit Mannigfaltigkeit bezeichnet
wird und einen Vektorraum 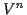 , so wird durch die Abbildung von
, so wird durch die Abbildung von 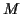 in
in 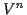 jeder Punkt einem Vektor zugeordnet. Die Zuordnung setzt eine
Ordnung des Raumes durch eine Vereinbarung über ein System voraus, das als Koordinatensystem
jeder Punkt einem Vektor zugeordnet. Die Zuordnung setzt eine
Ordnung des Raumes durch eine Vereinbarung über ein System voraus, das als Koordinatensystem
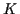 bezeichnet wird. Ein Koordinatensystem
bezeichnet wird. Ein Koordinatensystem 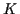 sei durch ein Paar
sei durch ein Paar
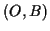 , welches aus einem festen Punkt
, welches aus einem festen Punkt 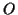 und einer
Basis
und einer
Basis 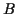 besteht, definiert. Von diesem ausgehend wird durch die bijektive
Abbildung
besteht, definiert. Von diesem ausgehend wird durch die bijektive
Abbildung
jedem Punkt 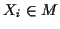 bezüglich
bezüglich  der Ortsvektor
der Ortsvektor
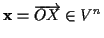 zugeordnet. (REINHARDT/SOEDER 1984) Zuerst wird jedoch vom Begriff des Vektors,
als einfachster Art einer Beschreibung der gegenseitigen Lage zweier Punkte
ausgegangen. Ein Vektor bezeichnet demnach eine Äquivalenzklasse parallelgleicher
Pfeile. Die Pfeile lassen sich als geordnete Punktepaare
zugeordnet. (REINHARDT/SOEDER 1984) Zuerst wird jedoch vom Begriff des Vektors,
als einfachster Art einer Beschreibung der gegenseitigen Lage zweier Punkte
ausgegangen. Ein Vektor bezeichnet demnach eine Äquivalenzklasse parallelgleicher
Pfeile. Die Pfeile lassen sich als geordnete Punktepaare
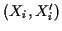 interpretieren, wobei
interpretieren, wobei 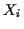 Angriffspunkte und
Angriffspunkte und 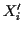 Zielpunkte
bezeichnen. Wichtig für den so eingeführten Begriff des Vektors ist dabei die
Unabhängigkeit dieses geometrischen Objektes vom gewählten Koordinatensystem1.1, d.h. seine Invarianz gegenüber bestimmten Basistransformationen. Um die Ordnung
des Raumes aufrechtzuerhalten reicht die Vereinbarung über ein gewähltes Koordinatensystem
nicht aus. Es müssen im weiteren Rechenregeln1.2 für die Elemente des Raumes
Zielpunkte
bezeichnen. Wichtig für den so eingeführten Begriff des Vektors ist dabei die
Unabhängigkeit dieses geometrischen Objektes vom gewählten Koordinatensystem1.1, d.h. seine Invarianz gegenüber bestimmten Basistransformationen. Um die Ordnung
des Raumes aufrechtzuerhalten reicht die Vereinbarung über ein gewähltes Koordinatensystem
nicht aus. Es müssen im weiteren Rechenregeln1.2 für die Elemente des Raumes 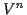 aufgestellt werden. Dabei gelten die
folgenden Gesetze:
aufgestellt werden. Dabei gelten die
folgenden Gesetze:
- Summe
-
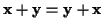
-
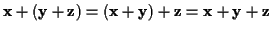
-
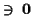 , so daß
, so daß
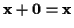
-
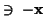 , zu jedem
, zu jedem 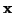 so daß
so daß
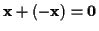
- gemischtes Produkt
-
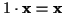
-
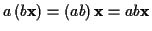
-
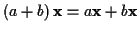
-
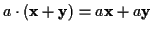
- Skalarprodukt
-
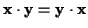
-
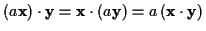
-
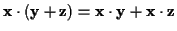
- Wenn
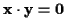 und
und 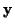 beliebig,
dann gilt
beliebig,
dann gilt
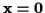
Sind nun die Gesetze 1, 2 und 3 erfüllt, so wird der Vektorraum 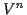 als Euklidscher Vektorraum bezeichnet, gelten nur 1 und 2 so bezeichnet
man ihn als Affinen Vektorraum.
als Euklidscher Vektorraum bezeichnet, gelten nur 1 und 2 so bezeichnet
man ihn als Affinen Vektorraum.
Da in den folgenden Abschnitten häufig die tensorielle Darstellung Verwendung
findet, soll hier zunächst ein kurzer Überblick gegeben werden. Dabei wird zwischen
skalaren und vektorwertigen Funktionen unterschieden und deren partielle Ableitungen
werden diskutiert. Die Einführung der Christoffelsymbole an dieser Stelle, dient
dem Herausstellen der Analogie zur kovarianten Behandlung von Bewegungsgleichungen
in der Form der Lagrangegleichungen zweiter Art. Die Darstellung der Funktionen
hält sich dabei weitestgehend an die von KLINGBEIL (1984) verwandte Notation.
Ein Index welcher nur der Unterscheidung von Objekten dient, wird als kovarianter
Index mit einem Punkt als Trennsymbol zu den Summationsindizes angefügt.
- Ein geometrischer Vektor
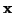 läßt sich nach der Summenkonvention
bezüglich der geradlinigen Basis
läßt sich nach der Summenkonvention
bezüglich der geradlinigen Basis
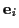 sowie der krummlinigen
Basis
sowie der krummlinigen
Basis
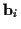 durch seine kontravarianten Komponenten wie folgt
darstellen
durch seine kontravarianten Komponenten wie folgt
darstellen
- skalarwertige Funktionen
- Für eine Skalarfunktion gilt bezüglich einer festen Basis
Nach der Vereinbarten Notation ergibt sich dann für die Ableitungen nach den
ko- bzw. kontravarianten Komponenten
Hierbei ist zu beachten, daß sich bei Ableitungen eines Skalars nach den im
allgemeinen kontravarianten Koordinaten die kovarianten Komponenten eines Vektors
(Tensor 1. Stufe) ergeben. Für das totale Differential gilt dann
- Wird nun eine ortsabhängige Basis
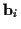 eingeführt,
so kann am Transformationsverhalten gezeigt werden, daß es sich bei
eingeführt,
so kann am Transformationsverhalten gezeigt werden, daß es sich bei 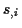 ebenfalls um (kovariante) Komponenten eines Tensors 1. Stufe handelt. Aus diesem
Grund wird eine s.g. kovariante Ableitung
ebenfalls um (kovariante) Komponenten eines Tensors 1. Stufe handelt. Aus diesem
Grund wird eine s.g. kovariante Ableitung
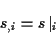 |
(1.1) |
eingeführt, welche durch ihre Eigenschaft der Invarianz gegenüber erlaubten
Parametertransformationen definiert ist.
- vektorwertige Funktionen
- Eine vektorwertige Funktion
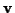 wird bezüglich einer festen kartesischen
Basis beschrieben durch
wird bezüglich einer festen kartesischen
Basis beschrieben durch
Für ihre Ableitungen nach den kartesischen Koordinaten ergibt sich dann
Und das totale Differential lautet in diesem Fall
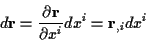 |
(1.2) |
mit
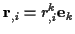 , wobei die
, wobei die 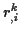 die gemischt ko/kontravarianten Komponenten eines Tensors zweiter Stufe bilden.
die gemischt ko/kontravarianten Komponenten eines Tensors zweiter Stufe bilden.
- Es sei nun
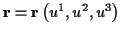 eine
vektorwertige Funktion der krummlinigen Koordinaten, so folgt analog
zu (
eine
vektorwertige Funktion der krummlinigen Koordinaten, so folgt analog
zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) für das totale Differential
) für das totale Differential
Für die Ableitung nach den kartesischen Koordinaten gilt aber aufgrund der
Kettenregel
so daß sich die ortsabhängige Basis
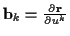 über
über
bzw. die kartesische Basis nach
bestimmen läßt. Im Gegensatz zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
kann aber gezeigt werden, daß im Falle eines Tensors erster oder höherer Stufe,
dessen partielle Ableitung kein Tensor mehr ist. Am Beispiel eines Tensors 1.
Stufe gilt
)
kann aber gezeigt werden, daß im Falle eines Tensors erster oder höherer Stufe,
dessen partielle Ableitung kein Tensor mehr ist. Am Beispiel eines Tensors 1.
Stufe gilt
Dies kommt daher, daß, wenn man bspw. die Ableitung eines Vektors in einem Punkt
des krummlinigen Raumes bestimmen will, man Informationen über den Raum selbst,
d.h. speziell über die Nachbarschaft des Punktes benötigt. Diese Informationen,
die einen Punkt im Raum mit den weiteren, den Raum bildenden Punkten verknüpft,
müssen sich aus der Metrik des Raumes ableiten lassen. Es ist nun möglich, aus
der geforderten Invarianz der Ableitungen, einen Korrekturterm für die partiellen
Ableitungen herzuleiten, so daß eine kovariante Ableitung im krummlinigen
Raum gefunden werden kann. Für eine vektorwertige Funktion ergibt sich diese
zu
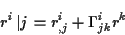 |
(1.3) |
wobei die
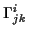 1.3 selbst keine Tensoreigenschaft besitzen. Mithilfe dieser Ableitung wird ein
Absolutes Differential über
1.3 selbst keine Tensoreigenschaft besitzen. Mithilfe dieser Ableitung wird ein
Absolutes Differential über
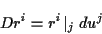 |
(1.4) |
definiert. Man kann zeigen, daß 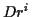 die Komponenten des vollständigen
Differentials bezüglich der krummlinigen Basis
die Komponenten des vollständigen
Differentials bezüglich der krummlinigen Basis
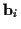 bildet,
d.h. es gilt dann
bildet,
d.h. es gilt dann
Nach dem theorema egregium von Gauß ist bekannt, daß die Krümmung einer
Fläche allein vom Metriktensor abhängt. Das bedeutet, am Beispiel einer in einem
dreidimensionalen kartesischen Raum eingebetteten Fläche, daß das Krümmungsmaß
dieser Fläche ohne Informationen bezüglich einer Einbettung, d.h. allein aus
Messungen auf der Fläche bestimmbar ist. Dies führte zu einer vom Einbettungsraum
unabhängigen Flächentheorie, deren Grundlagen in den folgenden Abschnitten kurz
aufgeführt sind.
Der von Riemann eingeführte verallgemeinerte Raumbegriff ist die Mannigfaltigkeit.
Die Definition einer solchen erfolgt über die Transformationsgleichungen zweier
Koordinatensysteme
Sind die Transformationsgleichungen stetig differenzierbar, so handelt es sich
bei der durch (1.5) und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) gegebenen Mannigfaltigkeit
um eine n-dimensionale differenzierbare Mannigfaltigkeit. In jedem
ihrer Punkt, können die totalen Differentiale der Koordinaten über
) gegebenen Mannigfaltigkeit
um eine n-dimensionale differenzierbare Mannigfaltigkeit. In jedem
ihrer Punkt, können die totalen Differentiale der Koordinaten über
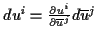 und umgekehrt bestimmt werden. Mit diesem Schritt erhält man die linearen Transformationen
der Koordinatendifferentiale über die für einen Tensor erster Stufe geltenden
Transformationskoeffizienten.
und umgekehrt bestimmt werden. Mit diesem Schritt erhält man die linearen Transformationen
der Koordinatendifferentiale über die für einen Tensor erster Stufe geltenden
Transformationskoeffizienten.
Abbildung:
Geometrische Interpretation des Affinen
Tangentialraums
|
|
Mit Hilfe des Tensorcharakters der Koordinatendifferentiale 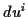 läßt
sich diesen in einem Punkt
läßt
sich diesen in einem Punkt 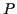 ein Vektor
ein Vektor 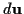 zuordnen.
zuordnen.
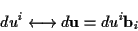 |
(1.7) |
Ordnet man einem zweiten Tensor (bzw. Koordinatendifferential) ebenfalls einen
Vektor 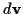 zu, so kann man durch Erklärung einer Vektorsumme
zu, so kann man durch Erklärung einer Vektorsumme
und eines Produktes mit einem Skalar 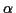
der Mannigfaltigkeit im Punkt 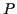 einen Vektorraum anhängen. Es wird vereinbart,
daß für die Elemente dieses Raumes, die Gesetze (1) und (2) aus Abschnitt 1.1.1.1
erfüllt sein sollen. Da kein Skalarprodukt erklärt ist, läßt sich nur ein affiner
Vektorraum anhängen. Abb.
einen Vektorraum anhängen. Es wird vereinbart,
daß für die Elemente dieses Raumes, die Gesetze (1) und (2) aus Abschnitt 1.1.1.1
erfüllt sein sollen. Da kein Skalarprodukt erklärt ist, läßt sich nur ein affiner
Vektorraum anhängen. Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) stellt eine geometrische
Interpretation dieses Vektorraumes dar. Es sei eine Raumkurve
stellt eine geometrische
Interpretation dieses Vektorraumes dar. Es sei eine Raumkurve
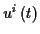 gegeben, außerdem existiert ein Punkt
gegeben, außerdem existiert ein Punkt 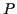 auf der Kurve, für den diese
den Parameterwert
auf der Kurve, für den diese
den Parameterwert 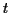 annimmt. Ein benachbarter Punkt
annimmt. Ein benachbarter Punkt 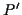 auf der
Kurve habe nun den Parameterwert
auf der
Kurve habe nun den Parameterwert 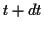 und die Koordinaten
und die Koordinaten
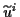 .
Dem Koordinatendifferential
.
Dem Koordinatendifferential
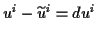 wird gemäß
(
wird gemäß
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) der Vektor
) der Vektor
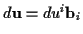 zugeordnet
zugeordnet 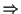 der Endpunkt des Vektors liegt nicht in
der Endpunkt des Vektors liegt nicht in 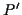 .
Außerdem entspricht dieser Vektor
.
Außerdem entspricht dieser Vektor 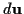 nur im Differentiellen
dem durch
nur im Differentiellen
dem durch
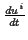 definierten Tangentenvektor an die Kurve.
definierten Tangentenvektor an die Kurve.
Dies führt zu dem Problem, daß einem Tensor in Form eines Koordinatendifferentials
der Mannigfaltigkeit, unterschiedliche Vektoren bezüglich der affinen Tangentialräume
zugeordnet werden. Die Tangentialräume in zwei verschiedenen Punkten sind in
diesem Fall nicht zusammenhängend.
Um zu einem geeigneten Zusammenhang zwischen den Räumen zu gelangen, ist es
notwendig die Parallelität von Vektoren im verallgemeinerten Raum auf andere
Weise zu definieren. Für eine gekrümmte Fläche, als Beispiel für eine zweidimensionale
Mannigfaltigkeit, läßt sich das Prinzip einfach verdeutlichen. Der affine Tangentialraum
in einem Punkt 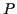 kann in einem solchen Fall mit der Tangentialebene an
die Fläche in diesem Punkt identifiziert werden. Versucht man einen Vektor
kann in einem solchen Fall mit der Tangentialebene an
die Fläche in diesem Punkt identifiziert werden. Versucht man einen Vektor 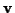 in der Tangentialebene in
in der Tangentialebene in 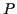 , parallel in einen benachbarten Punkt
, parallel in einen benachbarten Punkt 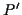 zu verschieben, so ist dies nach der euklidschen Definition von Parallelität,
aufgrund der Ortsabhängigkeit der Basisvektoren, nicht möglich. Eine 'parallelste'
Verschiebung kann jedoch auf diese Weise definiert werden, daß man
zu verschieben, so ist dies nach der euklidschen Definition von Parallelität,
aufgrund der Ortsabhängigkeit der Basisvektoren, nicht möglich. Eine 'parallelste'
Verschiebung kann jedoch auf diese Weise definiert werden, daß man 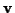 räumlich parallel (im euklidschen Sinn) nach
räumlich parallel (im euklidschen Sinn) nach 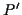 versetzt und diesen im
Anschluß daran in die Tangentialebene in
versetzt und diesen im
Anschluß daran in die Tangentialebene in 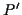 projeziert. Diese Parallelverschiebung
gilt natürlich nur für eine differentiell kleine Entfernung zwischen
projeziert. Diese Parallelverschiebung
gilt natürlich nur für eine differentiell kleine Entfernung zwischen 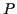 und
und 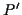 . Es kann gezeigt werden, daß diese Art der Verschiebung, der s.g.
Parallelverschiebung eines Tensors 1. Stufe nach Levi Civita entspricht.
. Es kann gezeigt werden, daß diese Art der Verschiebung, der s.g.
Parallelverschiebung eines Tensors 1. Stufe nach Levi Civita entspricht.
Ein Tensor 1. Stufe 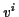 einer Mannigfaltigkeit heißt parallelverschoben
nach Levi Civita, entlang einer Kurve
einer Mannigfaltigkeit heißt parallelverschoben
nach Levi Civita, entlang einer Kurve
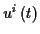 mit dem Parameter
mit dem Parameter
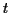 , wenn folgende Differentialgleichungen gelten
, wenn folgende Differentialgleichungen gelten
(d.h. sich sein absolutes Differential entlang der Kurve nicht ändert)
Mit (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) gilt die hierzu äquivalente Darstellung
) gilt die hierzu äquivalente Darstellung
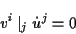 |
(1.8) |
Über (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) sind die Tangentialräume in den Punkten
) sind die Tangentialräume in den Punkten 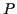 und
und 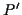 miteinander verknüpft. Wie leicht zu erkennen ist, entspricht
die Einführung der kovarianten Ableitung in (
miteinander verknüpft. Wie leicht zu erkennen ist, entspricht
die Einführung der kovarianten Ableitung in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) der Definition
eines verallgemeinerten Paralleltransportes. Beide Operationen verknüpfen die
affinen Tangentialräume und ermöglichen auf diese Weise die mathematische Beschreibung
von Objekten in der Mannigfaltigkeit. Da diese Verknüpfung, nach Einführung
einer Metrik, wie in (
) der Definition
eines verallgemeinerten Paralleltransportes. Beide Operationen verknüpfen die
affinen Tangentialräume und ermöglichen auf diese Weise die mathematische Beschreibung
von Objekten in der Mannigfaltigkeit. Da diese Verknüpfung, nach Einführung
einer Metrik, wie in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) zu sehen, über die Christoffelsymbole
geschieht, werden diese auch als Objekte des affinen Zusammenhangs
im Riemannschen Raum bezeichnet.
) zu sehen, über die Christoffelsymbole
geschieht, werden diese auch als Objekte des affinen Zusammenhangs
im Riemannschen Raum bezeichnet.
Der Riemannsche Raum entsteht durch die Ausstattung einer n-dimensionalen Mannigfaltigkeit
mit einem symmetrischen Tensorfeld
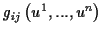 ,
so daß die Länge einer Kurve
,
so daß die Länge einer Kurve
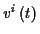 zwischen den Parameterwerten
zwischen den Parameterwerten
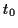 und
und 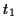 gegeben ist durch
gegeben ist durch
Durch die Einführung dieses Feldes, kann den Tangentialräumen über die Definition
eines Skalarproduktes
eine Euklidsche Metrik gegeben werden. Aus den partiellen Ableitungen des Metriktensors
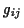 lassen sich dann, wie im folgenden noch gezeigt wird, die Christoffelsymbole
der zweiten Art
lassen sich dann, wie im folgenden noch gezeigt wird, die Christoffelsymbole
der zweiten Art
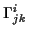 bestimmen. Sie sind die einzigen symmetrischen
Objekte des Zusammenhangs, die die Länge eines parallelverschobenen Vektors
unverändert lassen.
bestimmen. Sie sind die einzigen symmetrischen
Objekte des Zusammenhangs, die die Länge eines parallelverschobenen Vektors
unverändert lassen.
Eine Aufgabe der Geodäsie besteht in der Anlage von Lagefestpunktfeldern. Die
Bezugsfläche ist ein festgelegtes Rotationsellipsoid und die Lagekoordinaten
eines geodätischen Punktes werden, nach einer geeigneten Projektion desselben
auf das Bezugsellipsoid, in einem System Gaußscher Flächenparameter definiert.
Die numerischen Werte dieser Parameter entsprechen somit den Lagekoordinaten
der Punkte. Die am häufigsten Verwendung findenden Parametersätze können Tabelle
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) entnommen werden.
entnommen werden.
Da meist mehrere solcher Systeme nebeneinander Verwendung finden, ist es notwendig,
Flächenparametertransformationen zwischen den einzelnen Systemen durchzuführen.
Eine Möglichkeit dieser Transformation beruht auf der Differentialgleichung
der geodätischen Linie, d.h der i.A. eindeutigen, bezüglich eines Linienelementes
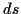 kürzesten, Verbindung zweier Punkte auf einer Fläche. Intuitiv ergeben
sich die Bedingungen für das Vorliegen einer kürzesten Verbindung zweier Punkte
entsprechend Abb.
kürzesten, Verbindung zweier Punkte auf einer Fläche. Intuitiv ergeben
sich die Bedingungen für das Vorliegen einer kürzesten Verbindung zweier Punkte
entsprechend Abb.![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) .
.
Abbildung:
Verlauf der geodätischen Linie auf einer gekrümmten
Fläche
|
|
Im kartesischen Koordinatenraum wird die kürzeste Verbindung zweier Punkte
mit den Ortsvektoren
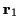 und
und
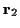 durch einen
Vektor
durch einen
Vektor
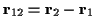 realisiert. Sind
diese beiden Punkte nun Elemente einer Fläche, so kann man direkt folgern, daß
die kürzeste Verbindung der Punkte über eine Flächenkurve durch die Projektion
der geradlinigen Verbindung
realisiert. Sind
diese beiden Punkte nun Elemente einer Fläche, so kann man direkt folgern, daß
die kürzeste Verbindung der Punkte über eine Flächenkurve durch die Projektion
der geradlinigen Verbindung
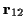 auf die Fläche erhalten wird.
Diese Projektion erfolgt so, daß jedem einzelnen Punkt von
auf die Fläche erhalten wird.
Diese Projektion erfolgt so, daß jedem einzelnen Punkt von
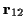 ein Lotfußpunkt auf der Fläche zugeordnet wird. Die Lotfußpunkte bilden dann
die geodätische Linie zwischen den beiden Punkten. Dies gilt streng genommen
nur für stetige Flächen. Außerdem gibt es auf beliebigen Flächen keine eindeutige
Zuordnung, da es mehrere geodätische Linien zwischen zwei Flächenpunkten geben
kann. Weiterhin kann eine Flächenkurve nur dann die kürzeste Verbindung zwischen
2 Punkten darstellen, wenn sie bezüglich der Fläche selbst keine Krümmung aufweist,
d.h. ihre Krümmung in jedem Punkt mit der Krümmumg der Fläche identisch ist.
Damit folgt, daß der Hauptnormalenvektor der geodätischen Linie in jedem Punkt
dem Normalenvektor der Fläche entspricht. In den beiden folgenden Abschnitten
wird nun die Bestimmungsleichung für den Verlauf der geodätischen Linie auf
verschiedene Weise hergeleitet. In der ersten Herleitung wird der Begriff der
Krümmung einer Verbindunglinie zweier Punkte auf gekrümmte Räume verallgemeinert
und damit die Differentialgleichung der geodätischen Linie als Bedingung für
eine bezüglich des gekrümmten Raumes krümmungslose Verbindung abgeleitet. In
der zweiten Herleitung sei die Analogie zwischen einer Geraden im kartesischen
Raum und der geodätischen Linie auf eine andere Weise herausgestellt. Die gesuchte
Differentialgleichung ergibt sich als Bedingung für den Paralleltransport eines
Tangenteneinheitsvektors. Anders ausgedrückt, ist die geodätische Linie die
Linie, analog zur Geraden im kartesischen Raum, entlang welcher der Tangenteneinheitsvektor
eine konstante Richtung besitzt.
ein Lotfußpunkt auf der Fläche zugeordnet wird. Die Lotfußpunkte bilden dann
die geodätische Linie zwischen den beiden Punkten. Dies gilt streng genommen
nur für stetige Flächen. Außerdem gibt es auf beliebigen Flächen keine eindeutige
Zuordnung, da es mehrere geodätische Linien zwischen zwei Flächenpunkten geben
kann. Weiterhin kann eine Flächenkurve nur dann die kürzeste Verbindung zwischen
2 Punkten darstellen, wenn sie bezüglich der Fläche selbst keine Krümmung aufweist,
d.h. ihre Krümmung in jedem Punkt mit der Krümmumg der Fläche identisch ist.
Damit folgt, daß der Hauptnormalenvektor der geodätischen Linie in jedem Punkt
dem Normalenvektor der Fläche entspricht. In den beiden folgenden Abschnitten
wird nun die Bestimmungsleichung für den Verlauf der geodätischen Linie auf
verschiedene Weise hergeleitet. In der ersten Herleitung wird der Begriff der
Krümmung einer Verbindunglinie zweier Punkte auf gekrümmte Räume verallgemeinert
und damit die Differentialgleichung der geodätischen Linie als Bedingung für
eine bezüglich des gekrümmten Raumes krümmungslose Verbindung abgeleitet. In
der zweiten Herleitung sei die Analogie zwischen einer Geraden im kartesischen
Raum und der geodätischen Linie auf eine andere Weise herausgestellt. Die gesuchte
Differentialgleichung ergibt sich als Bedingung für den Paralleltransport eines
Tangenteneinheitsvektors. Anders ausgedrückt, ist die geodätische Linie die
Linie, analog zur Geraden im kartesischen Raum, entlang welcher der Tangenteneinheitsvektor
eine konstante Richtung besitzt.
Für die Bestimmung der kürzesten Verbindung zweier Örter im dreidimensionalen
Raum gilt allgemein folgender Zusammenhang
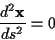 |
(1.9) |
Diese Gleichung beinhaltet, daß die Krümmung der durch
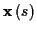 definierten Kurve Null ist. Das Linienelement
definierten Kurve Null ist. Das Linienelement
beschreibt in einem kartesischen Koordinatensystem die Rechenvorschrift zur
Bestimmung des Abstandes. Die Lösung von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergibt sich
nach zweifacher Integration zu
) ergibt sich
nach zweifacher Integration zu
der Punktrichtungsform der Geradendarstellung im 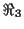 mit dem Parameter
mit dem Parameter
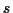 . Um zu einer allgemein gültigen Darstellung der Differentialgleichung
(
. Um zu einer allgemein gültigen Darstellung der Differentialgleichung
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) für beliebige n-dimensionale Koordinatensysteme zu
gelangen, muß
) für beliebige n-dimensionale Koordinatensysteme zu
gelangen, muß
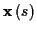 zweimal integriert werden. Für
zweimal integriert werden. Für
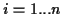 gilt nach dem totalen Differential
gilt nach dem totalen Differential
Nach der Summenkonvention ergibt sich
und nach der zweiten Differentiation
Die Multiplikation mit
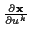 führt
zu
führt
zu
Hierin kann nun
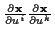 durch den Metriktensor
durch den Metriktensor 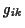 ersetzt werden. Um die totalen Differentiale
des Ortsvektors und der Basisvektoren des Dreibeins in die Basis zurückzuschreiben,
d.h. vom einbettenden Raum unabhängig zu werden, muß der Term
ersetzt werden. Um die totalen Differentiale
des Ortsvektors und der Basisvektoren des Dreibeins in die Basis zurückzuschreiben,
d.h. vom einbettenden Raum unabhängig zu werden, muß der Term
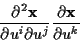 |
(1.10) |
durch eine nur von den krummlinigen Koordinaten abhängigen Größe ersetzt werden.
Mit der Gleichung
und zwei weiteren, welche durch zyklische Vertauschung aus der obigen abzuleiten
sind, erhält man nach einfacher Rechnung den folgenden Zusammenhang für (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
)
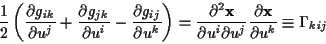 |
(1.11) |
Die mit 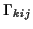 bezeichneten dreidimensionalen Felder werden als
Christoffelsymbole erster Art bezeichnet. Mit ihnen ergibt sich für
die Gleichung der kürzesten Verbindung zweier Punkte
bezeichneten dreidimensionalen Felder werden als
Christoffelsymbole erster Art bezeichnet. Mit ihnen ergibt sich für
die Gleichung der kürzesten Verbindung zweier Punkte
Über die Multiplikation mit den kontravarianten Metrikkoeffizienten und die
anschließende Einführung der Christoffelsymbole der zweiten Art
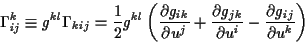 |
(1.12) |
läßt sich diese weiter vereinfachen zu
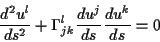 |
(1.13) |
Allgemein bedeutet eine parallele Verschiebung eines Vektors, daß Richtung und
Länge desselben von der Verschiebung unberührt bleiben. Im euklidschen Raum
bleibt ein Vektor und somit dessen kartesische Komponenten durch Paralleltransport
unverändert. Um diese Unveränderlichkeit mathematisch zu beschreiben, setzt
man das Differential des Vektors zu 0:
in allgemeinen Koordinaten gilt für diesen Vektor
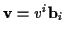 .
.
Für die Basisvektoren gilt:
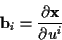 |
(1.14) |
Das totale Differential ergibt sich damit nach der Produktregel zu
Die Multiplikation mit den Basisvektoren und die Einführung des Metriktensors
führt dann zu
Mit dem totalen Differential der Basisvektoren
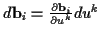 und (
und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) folgt
) folgt
Die rechte Seite der Gleichung entspricht (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
und kann dementsprechend durch die Christoffelsymbole der ersten Art ersetzt
werden. Dies führt analog zum vorigen Kapitel, nach Einführung der Christoffelsymbolen
zweiter Art, zur allgemeinen Form des Paralleltransportes eines kontravarianten
Vektors:
)
und kann dementsprechend durch die Christoffelsymbole der ersten Art ersetzt
werden. Dies führt analog zum vorigen Kapitel, nach Einführung der Christoffelsymbolen
zweiter Art, zur allgemeinen Form des Paralleltransportes eines kontravarianten
Vektors:
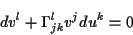 |
(1.15) |
Ist nun ein Tangentenvektor an eine Raumkurve
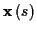 durch
durch
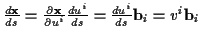 gegeben, dann folgt für dessen Parallelverschiebung, wenn
gegeben, dann folgt für dessen Parallelverschiebung, wenn
das Äquivalent zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) bezüglich
des Paralleltransportes entlang einer Kurve beschreibt direkt die Differentialgleichung
der geodätischen Linie:
) bezüglich
des Paralleltransportes entlang einer Kurve beschreibt direkt die Differentialgleichung
der geodätischen Linie:
Für beliebige orthogonale Flächenparametersysteme ergibt sich die Gleichung
der geodätischen Linie vereinfacht aus folgenden 3 Differentialgleichungen 1.
Ordnung:
Damit lassen sich die die Koordinaten eines beliebigen Punktes
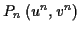 auf der geodätischen Linie, die im Pol
auf der geodätischen Linie, die im Pol
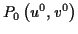 des lokalen geodätischen Polarkoordinatensystems den Richtungswinkel
des lokalen geodätischen Polarkoordinatensystems den Richtungswinkel 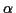 bezüglich der Parameterlinie
bezüglich der Parameterlinie  besitzt, in Abhängigkeit der Länge
der geodätischen Linie
besitzt, in Abhängigkeit der Länge
der geodätischen Linie 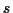 aus der Lösung von (
aus der Lösung von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) über
eine Taylorentwicklung nach
) über
eine Taylorentwicklung nach
bestimmen. Da die Ableitungen von 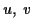 und
und 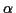 nach der
Bogenlänge Funktionen
nach der
Bogenlänge Funktionen
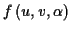 sind, ergeben sich
die Ableitungen höherer Ordnung durch schrittweises Anwenden der Kettenregel
am Beispiel für
sind, ergeben sich
die Ableitungen höherer Ordnung durch schrittweises Anwenden der Kettenregel
am Beispiel für
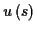 nach:
nach:
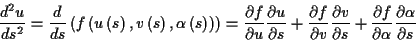 |
(1.17) |
Für beliebige Gauß'sche Flächenparametersysteme hängen die oben genannten Differentialquotienten
linear von
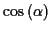 und
und
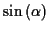 ab. Somit kann die Lösung der 1. geodätischen Hauptaufgabe als Reihenentwicklung
dargestellt werden:
ab. Somit kann die Lösung der 1. geodätischen Hauptaufgabe als Reihenentwicklung
dargestellt werden:
Nach Einführung der Riemannschen Normalkoordinaten
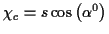 und
und
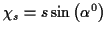 , ergeben sich die s.g.
Legendreschen Reihen
, ergeben sich die s.g.
Legendreschen Reihen
Der Wert für
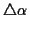 ist ebenfalls auf diese Weise bestimmbar,
jedoch existiert beim Beispiel der geographischen Koordinaten auf dem Rotationsellipsoid
eine strenge Rechenvorschrift, welche sich aus dem Satz von Clairaut
ableiten läßt und der Reihenentwicklung aus numerischen Gesichtspunkten vorzuziehen
ist:
ist ebenfalls auf diese Weise bestimmbar,
jedoch existiert beim Beispiel der geographischen Koordinaten auf dem Rotationsellipsoid
eine strenge Rechenvorschrift, welche sich aus dem Satz von Clairaut
ableiten läßt und der Reihenentwicklung aus numerischen Gesichtspunkten vorzuziehen
ist:
(wobei 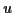 der geographischen Breite
der geographischen Breite 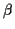 entspricht) Der Vollständigkeit
halber sei hier noch die Lösung der 2. geodätischen Hauptaufgabe, welche sich
aus der Umkehrung der Reihen mittels Reiheninversion ergibt, angegeben:
entspricht) Der Vollständigkeit
halber sei hier noch die Lösung der 2. geodätischen Hauptaufgabe, welche sich
aus der Umkehrung der Reihen mittels Reiheninversion ergibt, angegeben:
Die benötigten Koeffizienten ergeben sich nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) sukzessive
aus den Ableitungen. Die ersten Koeffizienten1.4 seien in den Tabellen (
) sukzessive
aus den Ableitungen. Die ersten Koeffizienten1.4 seien in den Tabellen (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) und (
) und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
kurz dargestellt.
)
kurz dargestellt.
Tabelle:
Koeffizienten der Legendreschen Reihe für 1.
geod. Hauptaufgabe
|
|
Tabelle:
Koeffizienten der Legendreschen Reihe für 2.
geod. Hauptaufgabe
|
|
Die Entwicklung immer schnellerer Rechenanlagen in den letzten 20 Jahren führte
dazu, daß die klassische Lösung der geodätischen Hauptaufgaben über die im vorigen
Abschnitt beschriebene Reihenentwicklung mehr und mehr in den Hintergrund trat.
Zwar weist sie bezüglich der Rechengeschwindigkeit Vorteile gegenüber numerischen
Verfahren auf, doch in Anbetracht der heutigen Prozessorleistungen von bis zu
1GHz, relativiert sich dies. Die numerische Integration kann nach Aufstellen
der Differentialgleichung der geodätischen Linie für jede beliebig gekrümmten
Fläche erfolgen, während die Lösung über eine Reihenentwicklung zunächst einen
großen Aufwandt an algebraischen Umformungen erfordert, der mit steigender Anforderung
an die Genauigkeit auch von heute erhältlichen Computer Algebra Systemen (CAS)
noch nicht in befriedigender Form durchgeführt werden kann.
Es steht eine Vielzahl verschiedener Integratoren1.5 zur numerischen Quadratur von Differentialgleichungen zur Verfügung. Diese
unterscheiden sich in der Zahl ihrer Funktionsaufrufe, sowie in der Zuverlässigkeit.
Einige arbeiten mit einer Fehlerschätzung, so daß sie, bei Vorgabe einer bestimmten
Genauigkeit, ohne großen Zeitverlust, die Zahl der nötigen Iterationen zur Einhaltung
der Vorgabe selbst abschätzen. An dieser Stelle sei auf das zweite Kapitel verwiesen,
das sich intensiver mit dieser Problematik auseinandersetzt.
In diesem zweiten Abschnitt des ersten Teils soll nun auf die Möglichkeiten
der Formulierung des Bewegungsproblems in der Mechanik eingegangen werden. Hierzu
seien zunächst kurz einige Begriffsdefinitionen aufgeführt. Im Anschluß daran
wird auf die alternativen Darstellungsformen der Bewegungsgleichungen nach Lagrange
und Hamilton eingegangen.
Ein Teilchen bewege sich entlang einer Bahn 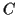 , dann ist seine Position
zur Zeit
, dann ist seine Position
zur Zeit 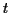 im Punkt
im Punkt 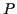 durch den Ortsvektor
durch den Ortsvektor
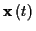 gekennzeichnet. Als Momentangeschwindigkeit des Teilchens im Punkt
gekennzeichnet. Als Momentangeschwindigkeit des Teilchens im Punkt 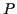 definiert man
definiert man
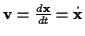 . Ist
der Ortsvektor gegeben durch
. Ist
der Ortsvektor gegeben durch
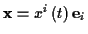 ,
so folgt für die Geschwindigkeit
,
so folgt für die Geschwindigkeit
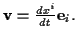 Der Betrag ergibt sich folglich zu
Der Betrag ergibt sich folglich zu
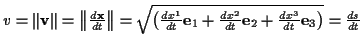 .
.
Als Beschleunigung eines Teilchens im Punkt  wird definiert
wird definiert
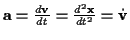 .
.
Greift an einem Körper der Masse 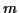 eine äußere Kraft
eine äußere Kraft 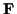 an und bewegt sich dieser infolge der Kraftwirkung mit der Geschwindigkeit
an und bewegt sich dieser infolge der Kraftwirkung mit der Geschwindigkeit 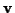 ,
dann gilt
,
dann gilt
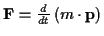 , bei
zeitunabhängiger Masse gilt dann das 2. Newtonsche Axiom
, bei
zeitunabhängiger Masse gilt dann das 2. Newtonsche Axiom
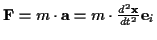 .
.
Bewirkt eine Kraft 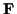 eine Verschiebung des Massepunktes um
eine Verschiebung des Massepunktes um 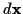 ,
dann leistet sie die Arbeit
,
dann leistet sie die Arbeit
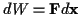 . Die gesamte Arbeit
die entlang eines Weges
. Die gesamte Arbeit
die entlang eines Weges 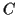 von einem Vektorfeld
von einem Vektorfeld 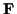 bei
der Bewegung eines Massepunktes verrichtet wird ergibt sich aus dem Kurvenintegral
bei
der Bewegung eines Massepunktes verrichtet wird ergibt sich aus dem Kurvenintegral
Die gesamte Arbeit bei der Bewegung eines Masseteilchens von 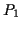 nach
nach
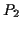 , wobei
, wobei 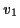 die Geschindigkeit zum Zeitpunkt
die Geschindigkeit zum Zeitpunkt 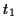 und
und 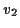 die zum Zeitpunkt
die zum Zeitpunkt 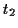 ist, ergibt sich nach
ist, ergibt sich nach
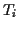 bezeichnet hier die kinetische Energie des Teilchens zu den jeweiligen
Zeitpunkten
bezeichnet hier die kinetische Energie des Teilchens zu den jeweiligen
Zeitpunkten 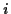 .
.
Unter der Annahme, es existiere eine Skalarfunktion 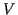 , so daß gilt
, so daß gilt
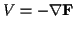 ,
beträgt die bei der Bewegung eines Massepunktes geleistete Arbeit
,
beträgt die bei der Bewegung eines Massepunktes geleistete Arbeit
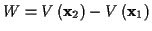 .
In diesem Fall ist die geleistete Arbeit unabhängig vom zurückgelegten Weg,
daher wird ein solches Kraftfeld, das sich aus einem Potential ableiten läßt
als konservatives Kraftfeld bezeichnet.
.
In diesem Fall ist die geleistete Arbeit unabhängig vom zurückgelegten Weg,
daher wird ein solches Kraftfeld, das sich aus einem Potential ableiten läßt
als konservatives Kraftfeld bezeichnet.
Folgende Bedingungen müssen erfüllt sein, damit ein konservatives Kraftfeld
vorliegt:
-

-
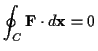
- Potentielle Energie oder Potential
Der Skalar 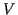 wird als potentielle Energie oder als Potential eines Teilchens
in einem konservativem Kraftfeld
wird als potentielle Energie oder als Potential eines Teilchens
in einem konservativem Kraftfeld 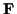 bezeichnet. Das Potential
ist nur bis auf eine additive Konstante festgelegt. Unter der Annahme
bezeichnet. Das Potential
ist nur bis auf eine additive Konstante festgelegt. Unter der Annahme 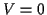 für
für
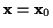 , gilt für dieses
, gilt für dieses
Für ein konservatives Kraftfeld gilt
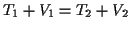 . Die Summe
aus kinetischer Energie und potentieller Energie wird als Gesamtenergie
. Die Summe
aus kinetischer Energie und potentieller Energie wird als Gesamtenergie 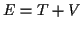 bezeichnet. In einem konservativem Kraftfeld ist die Gesamtenergie
bezeichnet. In einem konservativem Kraftfeld ist die Gesamtenergie 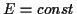 .
.
Im Allgemeinen wird bei der Formulierung von Bewegungsproblemen hauptsächlich
auf die Newton/Eulersche Bewegungsgleichung
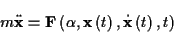 |
(1.18) |
zurückgegriffen. Wird hier das Kraftgesetz
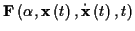 als quantitativer Einfluß der Umgebung auf einen Massepunkt vorgegeben, so liefert
(
als quantitativer Einfluß der Umgebung auf einen Massepunkt vorgegeben, so liefert
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) eine vektorielle Differentialgleichung 2. Ordnung
zur Bestimmung der Bahn
) eine vektorielle Differentialgleichung 2. Ordnung
zur Bestimmung der Bahn
 dieses Masseteilchens.
Die Herausstellung der Analogie zu den geodätischen Hauptaufgaben erfordert
aber eine andere Betrachtungsweise des Bewegungsproblems, so daß in den folgenden
Abschnitten zunächst drei weitere Methoden zur Lösung von Bewegungsproblemen
dargestellt werden.
dieses Masseteilchens.
Die Herausstellung der Analogie zu den geodätischen Hauptaufgaben erfordert
aber eine andere Betrachtungsweise des Bewegungsproblems, so daß in den folgenden
Abschnitten zunächst drei weitere Methoden zur Lösung von Bewegungsproblemen
dargestellt werden.
Innere und äußere Kräfte, die auf ein System von Massepunkten wirken, schränken
die Bewegungsmöglichkeiten der einzelnen Teilchen meist nicht ein. Je nach Wahl
der 6 Anfangswerte sind die Massepunkte in einem solchen Fall in der Lage, jeden
Punkt des Raumes zu erreichen. Die meisten Bewegungen verlaufen jedoch nicht
frei, d.h. die Massepunkte sind in ihrer Bewegung durch gewisse Nebenbedingungen
eingeschränkt. Diese Nebenbedingungen sind zunächst geometrischer Art, bspw.
kann als Nebenbedingung für die Bewegung eines starren Pendels, zum einen die
feste Schwingebene, zum anderen der kugelförmige mögliche Aufenthaltsraum des
Pendelkörpers festgelegt werden. Die Bewegung erfolgt dann entlang des Schnittes
der beiden geometrischen Körper. Man kann nun über die Formulierung der s.g.
Lagrangegleichung erster Art die Bewegungsgleichung lösen, indem man
virtuelle Zwangskräfte
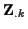 , d.h. Kräfte einführt, deren Wirkungslinien
senkrecht zur einschränkenden Geometrie stehen und somit keine Arbeit verrichten.
, d.h. Kräfte einführt, deren Wirkungslinien
senkrecht zur einschränkenden Geometrie stehen und somit keine Arbeit verrichten.
Dies ist äquivalent zum s.g D'Alembertschen Prinzip1.6:
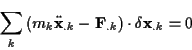 |
(1.19) |
Mit den Zwangskräften
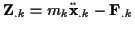 .
.
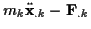 ist dabei so zu interpretieren,
daß sich die eingeprägte Kraft
ist dabei so zu interpretieren,
daß sich die eingeprägte Kraft
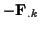 mit der Trägheitskraft
mit der Trägheitskraft
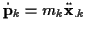 im Gleichgewicht befindet.
im Gleichgewicht befindet.
Die Zwangskräfte dienen nur der geometrischen Festlegung der Bewegung und tragen,
da sie keine Arbeit verrichten, nicht zur Bewegung selbst bei1.7. Allgemein lassen sich die Lagrangegleichungen erster Art in folgender Form
darstellen
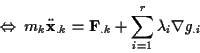 |
(1.20) |
Die Zwangskräfte 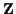 werden, wie bereits erwähnt, derart eingeführt,
daß sie orthogonal zur bewegungseinschränkenden Geometrie stehen, und somit
in (
werden, wie bereits erwähnt, derart eingeführt,
daß sie orthogonal zur bewegungseinschränkenden Geometrie stehen, und somit
in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) dargestellt werden können als Vektoren
) dargestellt werden können als Vektoren
in Richtung der Flächennormalen der restriktiven geometrischen Figuren, welche
in der impliziten Darstellung
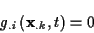 |
(1.21) |
gegeben sind.
Abbildung:
Körper gleitet unter Einfluß der Schwerkraft
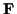 eine Ebene herab
eine Ebene herab
|
|
Beispiel:Ein Körper gleitet unter Einfluß
der Schwerkraft eine schiefe Ebene hinunter:
Wie in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zu sehen, bildet die Schnittgerade der schiefen
Ebene mit der
zu sehen, bildet die Schnittgerade der schiefen
Ebene mit der
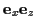 -Ebene den Winkel
-Ebene den Winkel 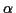 mit der
mit der
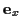 -Achse. Zum einen gilt daher zu jedem Zeitpunkt
-Achse. Zum einen gilt daher zu jedem Zeitpunkt
zum anderen
Für (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergibt sich in diesem Fall
) ergibt sich in diesem Fall
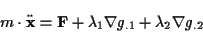 |
(1.22) |
Um die Multiplikatoren zu bestimmen, kann man, da die Nebenbedingungen nicht
explizit von der Zeit abhängen, d.h.
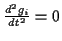 gilt,
man in diesem Fall die 2. Zeitableitungen der Nebenbedingungen über
gilt,
man in diesem Fall die 2. Zeitableitungen der Nebenbedingungen über
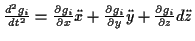 ermitteln. Es folgt dann
ermitteln. Es folgt dann
Aus (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergibt sich damit
) ergibt sich damit
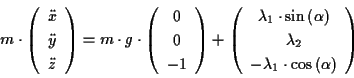 |
(1.25) |
Nach Einsetzen der zweiten Zeitableitungen der Koordinaten aus (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
in (
)
in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) entstehen die folgenden 3 Bestimmungsgleichungen
für die Lagrangemultiplikatoren
) entstehen die folgenden 3 Bestimmungsgleichungen
für die Lagrangemultiplikatoren 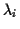 .
.
Die Ergebnisse werden nun in die allgemeine Lagrangegleichung 1. Art (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
eingesetzt und es ergibt sich
)
eingesetzt und es ergibt sich
Diese Gleichung läßt sich direkt integrieren. Nach der geeigneten Wahl der Konstanten
folgt die Bewegungsgleichung:
mit
Die Weiterentwicklung dieses Lösungsprinzips führt dann zu den Lagrangegleichungen
zweiter Art, sowie zum Hamiltonformalismus, die in den folgenden Abschnitten
eingehender behandelt werden.
Ein Ansatz, der ebenfalls auf Lagrange zurück geht, versucht die Bewegungsgleichung
zu lösen, indem der Lösungsraum durch die Einführung einer anderen Geometrie
eingeschränkt wird. Die Einführung der Geometrie erfolgt über die Definition
eines neuen Koordinatensystems, dessen Zahl unabhängiger Koordinaten eben der
Zahl der Freiheitsgrade des Systems von Massepunkten entspricht, für welche
die Bewegungsgleichungen zu lösen sind. Die Zahl der Freiheitsgrade 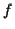 eines Systems entspricht dabei der Zahl der Koordinaten, die nötig sind, um
die Ortsfunktionen der Massepunkte des Systems zu beschreiben. Über das zu wählende
Koordinatensystem kann frei verfügt werden, jedoch bestimmt die Art des Systems
die Komplexität der Lösung des Bewegungsproblems. Die Zahl der Freiheitsgrade
verringert sich nun mit der Zahl der gegebenen Nebenbedingungen. Die minimal
zur Beschreibung des Problems notwendigen Koordinaten werden als generalisierte
Koordinaten1.8
eines Systems entspricht dabei der Zahl der Koordinaten, die nötig sind, um
die Ortsfunktionen der Massepunkte des Systems zu beschreiben. Über das zu wählende
Koordinatensystem kann frei verfügt werden, jedoch bestimmt die Art des Systems
die Komplexität der Lösung des Bewegungsproblems. Die Zahl der Freiheitsgrade
verringert sich nun mit der Zahl der gegebenen Nebenbedingungen. Die minimal
zur Beschreibung des Problems notwendigen Koordinaten werden als generalisierte
Koordinaten1.8
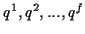 bezeichnet. Die Bewegung muß in diesen Koordinaten
zwangsfrei verlaufen. Ein System von
bezeichnet. Die Bewegung muß in diesen Koordinaten
zwangsfrei verlaufen. Ein System von 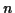 Massepunkten in einem 3-D Raum
wird durch
Massepunkten in einem 3-D Raum
wird durch 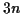 kartesische Koordinaten
kartesische Koordinaten
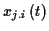 für
für 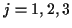 und
und 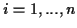 beschrieben. Sei
beschrieben. Sei 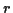 die Zahl der
Randbedingungen, so ergibt sich die Zahl der Freiheitsgrade des Systems nach
die Zahl der
Randbedingungen, so ergibt sich die Zahl der Freiheitsgrade des Systems nach
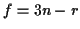 . Hieraus folgt, daß im Falle
. Hieraus folgt, daß im Falle 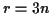 die Bewegung des Punktsystems
durch die Bedingungsgleichungen eindeutig bestimmt ist.
die Bewegung des Punktsystems
durch die Bedingungsgleichungen eindeutig bestimmt ist.
Der Zusammenhang zwischen den rechtwinkligen kartesischen und den generalisierten
Koordinaten eines Massepunktes 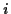 läßt sich wie folgt darstellen
läßt sich wie folgt darstellen
Bei diesen Gleichungen ist zu beachten, daß die Transformationsformeln stetig
sind und ebenfalls stetige Ableitungen besitzen1.9. Man klassifiziert1.10 nun verschiedene mechanische Systeme folgendermaßen:
- skleronome und rheonome Systeme
- skleronom: explizite Zeitabhängigkeit in den Transformationsgleichungen
- rheonom: keine explizite Zeitabhängigkeit
- holonom und nichtholonome Systeme
- holonom: Nebenbedingungen lassen sich in der Form
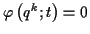 für
für 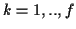 darstellen
darstellen
- nichtholonom andernfalls
- konservative und nicht konservative Systeme
- konservativ: alle auf ein System wirkenden Kräfte lassen sich aus einer Potentialfunktion
herleiten
- andernfalls
In den folgenden beiden Abschnitten werden die Lagrangegleichungen zweiter Art
auf verschiedene Arten hergeleitet. Die erste Herleitung geht von den Lagrangegleichungen
erster Art aus. Die zweite verfolgt einen Ansatz über das Variationsproblem.
Bei dieser wird der Beweis zunächst nur für Integrale der Form
angegeben, das Ergebnis ist jedoch leicht auf die in diesem Zusammenhang auftretenden
Integrale der Form
zu übertragen.
Der Ortsvektor eines Massepunktes 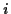 bezüglich des rechtwinklig kartesischen
Sytems ist gegeben durch
bezüglich des rechtwinklig kartesischen
Sytems ist gegeben durch
Unter der Annahme, daß sich die generalisierten Koordinaten eines Massepunktes
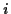 sich aufgrund einer geleisteten Arbeit
sich aufgrund einer geleisteten Arbeit 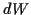 um
um 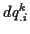 verändern, folgt für die daraus entstehende Verschiebung
verändern, folgt für die daraus entstehende Verschiebung
Für die geleistete Arbeit in einem System von 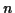 Massepunkten ergibt sich
nach
Massepunkten ergibt sich
nach
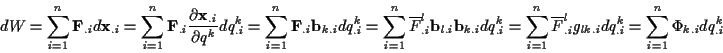 |
(1.26) |
mit 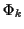 als der mit der ortsabhängigen Koordinate
als der mit der ortsabhängigen Koordinate 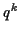 assozierten generalisierten Kraft, welche bestimmt werden kann über
assozierten generalisierten Kraft, welche bestimmt werden kann über
Für einen Massepunkt 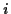 folgt aus (
folgt aus (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) und mit
dem totalen Differential
) und mit
dem totalen Differential
Übertragen auf ein System von Massepunkten ergibt sich damit ein Gleichungssystem
in dem, da die 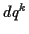 unabhängig voneinander sind, die Koeffizienten
unabhängig voneinander sind, die Koeffizienten
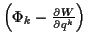 alle Null
sein müssen.
alle Null
sein müssen.
Die totale kinetische Energie eines Systems ergibt sich nach
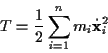 |
(1.27) |
oder als quadratische Form der generalisierten Geschwindigkeiten für den skleronomen
Fall zu
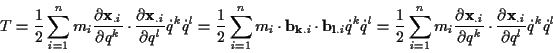 |
(1.28) |
Im Folgenden werden zwei zur Herleitung der Lagrange-Gleichungen notwendige
Rechenregeln abgeleitet:
- Kürzen von Produkten
In verallgemeinerten Koordinaten gilt für die Geschwindigkeit aufgrund der Kettenregel
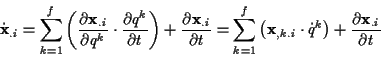 |
(1.29) |
Die Ableitung nach den generalisierten Geschwindigkeiten führt zum gesuchten
Zusammenhang
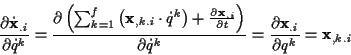 |
(1.30) |
- Vertauschen von Operatoren
Nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) folgt
) folgt
Es ergibt sich dann unter der Voraussetzung, daß die zweiten partiellen Ableitungen
von
 stetig sind:
stetig sind:
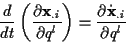 |
(1.31) |
Der Sinn der Einführung der neuen Koordinaten liegt nun darin, daß man die Nebenbedingungen
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) für die Lagrangegleichungen der ersten Art auch
interpretieren kann als Gleichungen von
) für die Lagrangegleichungen der ersten Art auch
interpretieren kann als Gleichungen von
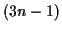 -dimensionalen
Hyperflächen in einem, durch die Punkte des mechanischen Systems definierten
-dimensionalen
Hyperflächen in einem, durch die Punkte des mechanischen Systems definierten
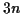 -dimensionalen Konfigurationsraum. Der Schnitt der Hyperflächen bildet
einen
-dimensionalen Konfigurationsraum. Der Schnitt der Hyperflächen bildet
einen 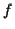 -dimensionalen Riemannschen Teilraum mit den Parametern
-dimensionalen Riemannschen Teilraum mit den Parametern 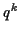 .
Dieser ist der Lösungsraum des Bewegungsproblems, mit anderen Worten, es ist
der Raum, der noch von den Bahnkurven der Massepunkte erreichbar ist.
.
Dieser ist der Lösungsraum des Bewegungsproblems, mit anderen Worten, es ist
der Raum, der noch von den Bahnkurven der Massepunkte erreichbar ist.
Wenn man die Lagrangegleichungen der ersten Art in den generalisierten Koordinaten
ausdrückt, so fallen die Zwangskräfte weg. Dies liegt daran, daß durch Anwenden
der Kettenregel bei der Ableitung von
nach den generalisierten Koordinaten zwei zueinander senkrecht stehende vektorielle
Funktion entstehen, die miteinander skalar multipliziert werden. Zum einen ergeben
sich Vektoren in Richtung der Flächennormalen der durch
definierten Nebenbedingungen, zum anderen ergeben sich die Tangentenvektoren
an den, durch die Parameter 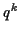 definierten Lösungsraum der Bewegung.
definierten Lösungsraum der Bewegung.
Die Darstellung von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) in generalisierten
Koordinaten lautet
) in generalisierten
Koordinaten lautet
Hierin entsprechen die
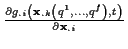 den senkrecht zu der durch die Nebenbedingung definierten Fläche stehenden Vektoren,
während die
den senkrecht zu der durch die Nebenbedingung definierten Fläche stehenden Vektoren,
während die
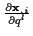 die Tangentenvektoren
an den Lösungsraum sind. Damit gilt
die Tangentenvektoren
an den Lösungsraum sind. Damit gilt
und die Darstellung der Bewegungsgleichung in den generalisierten Koordinaten
reduziert sich auf die Erweiterung der Newton/Eulerschen Bewegungsgleichung
mit
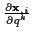 . Die Herleitung der
Lagrangegleichungen der zweiten Art folgt dann über
. Die Herleitung der
Lagrangegleichungen der zweiten Art folgt dann über
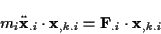 |
(1.32) |
Wendet man die Produktregel und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) an so gilt
allgemein
) an so gilt
allgemein
Nach Umstellung und Multiplikation mit 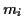 folgt mit (
folgt mit (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
unter Annahme der Konstanz der Masse
)
unter Annahme der Konstanz der Masse
Die rechte Seite der obigen Gleichung entspricht dabei der generalisierten Kraft
(vgl. (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )):
)):
Nach der Summation über alle Massepunkte folgt:
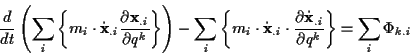 |
(1.33) |
mit (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) und (
) und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergibt sich andererseits
) ergibt sich andererseits
was eingesetzt in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) zu den Lagrangeschen
Bewegungsgleichungen zweiter Art führt :
) zu den Lagrangeschen
Bewegungsgleichungen zweiter Art führt :
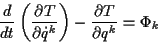 |
(1.34) |
Falls sich die generalisierten Kräfte aus einer Potentialfunktion nach
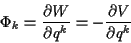 |
(1.35) |
herleiten lassen, wobei das Potential eine reine Ortsfunktion
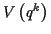 ist, kann man, mit Einführung der Lagrangefunktion
ist, kann man, mit Einführung der Lagrangefunktion
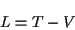 |
(1.36) |
für (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) schreiben
) schreiben
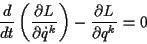 |
(1.37) |
Ein dem differentiellen D'Alembertschen Prinzip gleichwertiges, integrales
Prinzip ergibt sich aus der Integration der s.g. Lagrangeschen Zentralgleichung1.11. Es handelt sich um das Hamiltonsche Prinzip1.12:
Ein konservatives mechanisches System bewegt sich zwischen den Zeitpunkten 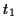 und
und 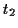 so, daß das s.g. Wirkungsintegral
so, daß das s.g. Wirkungsintegral
ein Extremum1.13 annimmt. Anders ausgedrückt gilt
mit 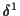 als Zeichen für die erste Variation.
als Zeichen für die erste Variation.
Wie schon zuvor für das D'Alembertsche Prinzip, können auch hier die Lagrangegleichungen
zweiter Art abgeleitet werden. Der Einfachheit halber sei dies im folgenden,
wie bereits erwähnt, für Funktionen des Typs
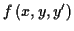 dargelegt.
dargelegt.
Gesucht ist die Bedingung die eingehalten werden muß, damit ein Integral der
Art
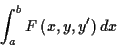 |
(1.38) |
Extremwerte animmt. Dazu sei zunächst eine Kurve durch
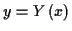 im Intervall
im Intervall 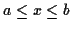 vorgegeben welche durch die Punkte
vorgegeben welche durch die Punkte
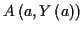 und
und
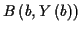 verläuft. Eine benachbarte Kurve,
ebenfalls durch
verläuft. Eine benachbarte Kurve,
ebenfalls durch 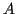 und
und 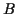 kann dann durch
kann dann durch
unter der Nebenbedingung
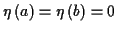 gegeben sein.
gegeben sein. 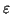 sei in diesem Fall ein von
sei in diesem Fall ein von 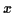 unabhängiger
Parameter. Das zu (
unabhängiger
Parameter. Das zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) äquivalente Integral der benachbarten
Kurve lautet damit
) äquivalente Integral der benachbarten
Kurve lautet damit
Die Bedingung für ein Extremum ist dann
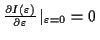 . Nach der Durchführung der Differentiation unter dem Integral, ergibt sich
die notwendige Bedingung zu
. Nach der Durchführung der Differentiation unter dem Integral, ergibt sich
die notwendige Bedingung zu
Partielle Integration führt dann zu
Da 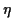 beliebig gewählt werden darf, gilt entsprechend auch
beliebig gewählt werden darf, gilt entsprechend auch
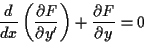 |
(1.39) |
(s.g Eulersche Gleichung)
Das Prinzip der Lösung von Bewegungsproblemen über die Lagrangegleichungen zweiter
Art sei am, schon bei den Lagrangegleichungen erster Art besprochenen, einfachen
Beispiel eines, eine schiefe Ebene reibungslos herabgleitenden Körpers, dargestellt.
Wie in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ersichtlich, kann im vorliegenden kartesischen
Koordinatensystem
ersichtlich, kann im vorliegenden kartesischen
Koordinatensystem
![\( \left[ \mathbf{e}_{x},\mathbf{e}_{y},\mathbf{e}_{z}\right] \)](img338.gif) eine generalisierte Koordinate
eine generalisierte Koordinate 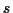 eingeführt werden, die die Bewegung
des Körpers ausreichend beschreibt. In diesem Fall ist leicht erkennbar, daß
das System nur einen Freiheitsgrad besitzt und somit eine generalisierte
Koordinate zur Beschreibung der Bewegung ausreicht. Die Koordinate
eingeführt werden, die die Bewegung
des Körpers ausreichend beschreibt. In diesem Fall ist leicht erkennbar, daß
das System nur einen Freiheitsgrad besitzt und somit eine generalisierte
Koordinate zur Beschreibung der Bewegung ausreicht. Die Koordinate 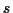 unterliegt keinerlei Zwängen, d.h. sie kann je nach Wahl der Anfangsbedingungen
jeden Wert annehmen. Die Transformationsgleichungen lauten in diesem Fall
unterliegt keinerlei Zwängen, d.h. sie kann je nach Wahl der Anfangsbedingungen
jeden Wert annehmen. Die Transformationsgleichungen lauten in diesem Fall
Nun wird zur Lösung des Problems die Lagrangefunktion nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
aufgestellt. Für die kinetische Energie ergibt sich
)
aufgestellt. Für die kinetische Energie ergibt sich
Die potentielle Energie ist gegeben durch
Die Lagrangefunktion lautet somit
und mit
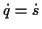 und
und 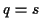 ergibt sich für (
ergibt sich für (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
)
Daraus ergibt sich die folgende Differentialgleichung zweiter Ordnung
Die Integration führt schließlich zur Bewegungsgleichung:
Mit Hilfe des Lagrangeformalismus kann man die Zahl, der für das Bewegungsproblem
zu lösenden Differentialgleichungen von 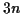 auf
auf
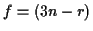 reduzieren. Jedoch bleibt hier das Problem Konstanten der Bewegung zu bestimmen,
die in der Form einer Differentialgleichung erster Ordnung vom Typ
reduzieren. Jedoch bleibt hier das Problem Konstanten der Bewegung zu bestimmen,
die in der Form einer Differentialgleichung erster Ordnung vom Typ
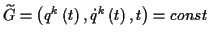 die Gesamtordnung des Systems jeweils um
die Gesamtordnung des Systems jeweils um 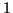 verringern. Man kann zwar
durch Betrachten von
verringern. Man kann zwar
durch Betrachten von 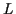 , zyklische Koordinaten bestimmen, d.h. Koordinaten,
von der die Lagrangefunktion nicht explizit abhängt1.14, aber dieses Verfahren ist recht umständlich. Um das Problem zu vereinfachen,
führt man zusätzlich weitere Koordinaten so ein, daß diese konstant werden,
wenn die ihnen zugehörige generalisierte Koordinate zyklisch wird. Nach (
, zyklische Koordinaten bestimmen, d.h. Koordinaten,
von der die Lagrangefunktion nicht explizit abhängt1.14, aber dieses Verfahren ist recht umständlich. Um das Problem zu vereinfachen,
führt man zusätzlich weitere Koordinaten so ein, daß diese konstant werden,
wenn die ihnen zugehörige generalisierte Koordinate zyklisch wird. Nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
ist dies der Fall bei den generalisierten Impulsen
)
ist dies der Fall bei den generalisierten Impulsen
Die Erweiterung des Lösungsraumes auf einen 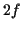 -dimensionalen Raum1.15 mit den Koordinaten
-dimensionalen Raum1.15 mit den Koordinaten
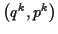 für
für 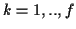 führt
zur s.g. Hamilton Theorie mit der eine Möglichkeit gegeben wird, zyklische
Koordinaten und damit Konstanten der Bewegung auf einfache Weise zu bestimmen.
führt
zur s.g. Hamilton Theorie mit der eine Möglichkeit gegeben wird, zyklische
Koordinaten und damit Konstanten der Bewegung auf einfache Weise zu bestimmen.
Die Definition der Hamiltonfunktion mit Hilfe der Lagrangefunktion
lautet
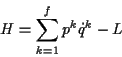 |
(1.40) |
Diese Funktion entspricht im Falle eines konservativen Systems, der gesamten
Energie
dieses Systems. Damit ist ersichtlich, daß es sich bei (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ),
unter Voraussetzung daß die potentielle Energie unabhängig von der Zeit ist,
nur um eine Form des Energieerhaltungsatzes handelt. Allgemein sollte die Hamiltonfunktion
sich mit Hilfe der Lagrangegleichungen als eine Funktion der generalisierten
Koordinaten und der generalisierten Impulse
),
unter Voraussetzung daß die potentielle Energie unabhängig von der Zeit ist,
nur um eine Form des Energieerhaltungsatzes handelt. Allgemein sollte die Hamiltonfunktion
sich mit Hilfe der Lagrangegleichungen als eine Funktion der generalisierten
Koordinaten und der generalisierten Impulse
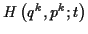 darstellen lassen. Man kann nun die Bewegungsgleichungen auf folgende Weise
in symmetrischer Form angeben
darstellen lassen. Man kann nun die Bewegungsgleichungen auf folgende Weise
in symmetrischer Form angeben
Diese Gleichungen werden als kanonische oder Hamiltonsche Bewegungsgleichungen
bezeichnet. Die Symmetrie der Impuls- und Ortskoordinaten ist leicht zu erkennen.
Jede zyklische Koordinate 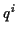 für die gilt
für die gilt
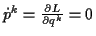 verringert nun die Ordnung der kanonischen Gleichungen um 2. Diese zyklische
Koordinate läßt sich durch direkte Integration bestimmen. Ist es nun möglich,
durch eine Koordinatentransformation alle
verringert nun die Ordnung der kanonischen Gleichungen um 2. Diese zyklische
Koordinate läßt sich durch direkte Integration bestimmen. Ist es nun möglich,
durch eine Koordinatentransformation alle 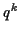 zyklisch zu machen, so
ist das Bewegungsproblem auf die Integration von
zyklisch zu machen, so
ist das Bewegungsproblem auf die Integration von 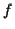 Bestimmungsgleichungen
der
Bestimmungsgleichungen
der 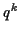 zurückgeführt. Der Vorteil des Hamiltonformalismus besteht
nun darin, daß es möglich ist aufgrund der Symmetrie, durch Einführung neuer
Koordinaten bzw. über Koordinatentransformationen, zyklische Koordinaten auf
einfache Weise zu ermitteln. Jedoch ist die kanonische Darstellung nicht invariant
bezüglich beliebiger Transformationen ,wie es bei den Lagrangeschen
Gleichungen zweiter Art der Fall ist. Eine Transformation, für die die kanonische
Darstellung invariant ist, wird als kanonische Transformation bezeichnet.
Seien die neuen Koordinaten durch
zurückgeführt. Der Vorteil des Hamiltonformalismus besteht
nun darin, daß es möglich ist aufgrund der Symmetrie, durch Einführung neuer
Koordinaten bzw. über Koordinatentransformationen, zyklische Koordinaten auf
einfache Weise zu ermitteln. Jedoch ist die kanonische Darstellung nicht invariant
bezüglich beliebiger Transformationen ,wie es bei den Lagrangeschen
Gleichungen zweiter Art der Fall ist. Eine Transformation, für die die kanonische
Darstellung invariant ist, wird als kanonische Transformation bezeichnet.
Seien die neuen Koordinaten durch
gegeben, und gibt es eine neue Funktion 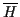 , so daß
, so daß
gilt, dann existiert eine Lagrangefunktion 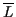 , für die dann
folgt
, für die dann
folgt
Aus dem Hamiltonschen Prinzip
läßt sich eine notwendige Existenz einer s.g. Erzeugenden Funktion
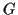 mit
mit
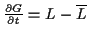 ableiten. Hängt
diese von
ableiten. Hängt
diese von 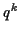 ,
,
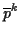 und
und 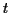 ab, so wird sie
mit
ab, so wird sie
mit
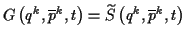 bezeichnet. Hier gilt dann
bezeichnet. Hier gilt dann
Wenn man nun erreicht, daß
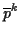 und
und
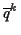 zyklische Variablen werden, so läßt sich, wie zuvor bereits erwähnt, das mechanische
Problem einfach lösen. Es existiert in Form der Hamilton-Jacobischen
Gleichung eine Bedingung für die s.g. Erzeugende Funktion einer solchen
kanonischen Transformation. Um das Bewegungsproblem zu lösen, wird eine Funktion
zyklische Variablen werden, so läßt sich, wie zuvor bereits erwähnt, das mechanische
Problem einfach lösen. Es existiert in Form der Hamilton-Jacobischen
Gleichung eine Bedingung für die s.g. Erzeugende Funktion einer solchen
kanonischen Transformation. Um das Bewegungsproblem zu lösen, wird eine Funktion
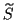 derart bestimmt, daß sie die Bedingung
derart bestimmt, daß sie die Bedingung
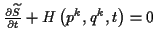 oder
oder
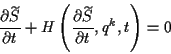 |
(1.41) |
erfüllt. Die Lösung kann in der Form
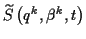 erhalten werden, dabei bezeichnen die
erhalten werden, dabei bezeichnen die 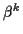 die übrigen
die übrigen 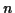 freien Parameter1.16, welche bis auf eine gemeinsame additive Konstante festgelegt sind. Die Ortskoordinaten
freien Parameter1.16, welche bis auf eine gemeinsame additive Konstante festgelegt sind. Die Ortskoordinaten
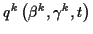 können über
können über
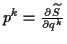 und
und
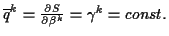 bestimmt werden. Falls die Hamiltonfunktion nicht explizit von der Zeit abhängt,
läßt sich der von der Zeit unabhängige Teil der Erzeugenden, nach Separation
der Variablen, schreiben als
bestimmt werden. Falls die Hamiltonfunktion nicht explizit von der Zeit abhängt,
läßt sich der von der Zeit unabhängige Teil der Erzeugenden, nach Separation
der Variablen, schreiben als
Damit vereinfacht sich die Hamilton-Jacobische Gleichung zu
worin 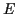 die Gesamtenergie des Systems bezeichnet.
die Gesamtenergie des Systems bezeichnet.
Die Differentialgleichung der geodätischen Linie kann nun, nach den in den vorigen
Abschnitten beschriebenen Verfahren, abgeleitet werden. Die Eigenschaft der
geodätischen Linie, die kürzeste Verbindung in beliebigen, durch ihre Metrik
ausgezeichneten Riemannschen Räumen darzustellen, führt zu einer Möglichkeit
der Ableitung ihrer Bestimmungsgleichung über die Minimierung des durch
gegebenen Abstandsmaßes. Eingesetzt1.17 in
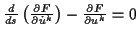 ergibt sich, wenn zunächst
ergibt sich, wenn zunächst 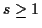 angenommen wird und somit die Wurzel
vernachlässigt werden kann,
angenommen wird und somit die Wurzel
vernachlässigt werden kann,
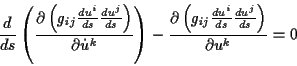 |
(1.42) |
Nach Umordnung folgt dann
Jetzt werden wieder die Christoffelsymbole der ersten Art eingeführt und analog
zu den in den vorigen Kapiteln beschriebenen Verfahren ergibt sich die folgende
Differentialgleichung als Bestimmungsgleichung1.18 für den Verlauf der geodätischen Linie im durch 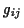 definierten Riemannschen
Raum.
definierten Riemannschen
Raum.
In den vorhergegangenen Abschnitten wurde zum einen die Herleitung der Lagrangeschen
Gleichungen aus der Erweiterung der Newton/Eulerschen Bewegungsgleichung in
generalisierten Koordinaten aufgezeigt, zum anderen wurde gezeigt, daß die Bedingungsgleichungen
des Variationsproblems
den Differentialgleichungen der geodätischen Linie ebenso äquivalent, sind
wie auch den Lagrangegleichungen der zweiten Art. Es handelt sich also bei der
Lösung der geodätischen Hauptaufgaben, wie auch bei der Lösung der Bewegungsgleichung
über die Lagrangegleichungen der zweiten Art, um eine Lösung desselben Problems.
Um die Analogie etwas besser herausstellen zu können, sei an dieser Stelle die
Herleitung der expliziten Form der Lagrangegleichungen über die Einführung der
generalisierten Koordinaten angeführt. Dieses schon zuvor beschriebene Verfahren,
das Bewegungsproblem über eine Einschränkung des Lösungsraumes, durch die Wahl
von generalisierten Koordinaten, zu vereinfachen, formuliert das mechanische
Problem in einer 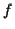 -dimensionalen differenzierbaren Mannigfaltigkeit.
Über die Einführung einer Metrik wird diese Mannigfaltigkeit zu einem Riemannschen
Raum. Die Bedingung welche die Metrik erfüllen muß, ist an die Existenz eines
symmetrischen Tensorfeldes
-dimensionalen differenzierbaren Mannigfaltigkeit.
Über die Einführung einer Metrik wird diese Mannigfaltigkeit zu einem Riemannschen
Raum. Die Bedingung welche die Metrik erfüllen muß, ist an die Existenz eines
symmetrischen Tensorfeldes
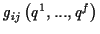 gebunden,
so daß sich die Länge einer Kurve zwischen 2 Parameterwerten
gebunden,
so daß sich die Länge einer Kurve zwischen 2 Parameterwerten 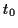 und
und
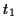 berechnet läßt nach
berechnet läßt nach
Wie in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) gezeigt, erfüllt die
kinetische Energie diese Forderung, so daß man einen Metriktensor der Form
) gezeigt, erfüllt die
kinetische Energie diese Forderung, so daß man einen Metriktensor der Form
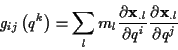 |
(1.43) |
einführen kann. Hieraus ergibt sich die Transformation
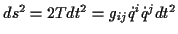 wobei das auftretende Linienelement
wobei das auftretende Linienelement 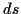 als kinematisches Linienelement
bezeichnet wird. Das Hamiltonsche Prinzip besagt, daß falls ein konservatives
System vorliegt und sich daher die Massenkräfte nach (
als kinematisches Linienelement
bezeichnet wird. Das Hamiltonsche Prinzip besagt, daß falls ein konservatives
System vorliegt und sich daher die Massenkräfte nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
berechnen lassen, die erste Variation von (
)
berechnen lassen, die erste Variation von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) verschwindet.
Die Lagrangefunktion
) verschwindet.
Die Lagrangefunktion 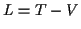 ergibt sich dann mit (
ergibt sich dann mit (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
und
)
und
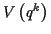 zu
zu
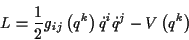 |
(1.44) |
Setzt man diese in die Eulerschen Gleichungen ein, so folgt analog zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
)
Wie leicht ersichtlich, ergibt sich dann
Diese Gleichung entspricht (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ), damit gilt für den
kräftefreien Fall, d.h. für den Fall mit Potential
), damit gilt für den
kräftefreien Fall, d.h. für den Fall mit Potential 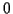 die Differentialgleichung
der geodätischen Linie:
die Differentialgleichung
der geodätischen Linie:
Somit ist die Lösung der Differentialgleichung der geodätischen Linie vollkommen
analog zur Lösung der Bewegungsgleichung eines Massepunktes auf einer Fläche
mit dem Potential Null und der Bogenlänge  als unabhängigem Parameter.
Dies führt dazu, daß Lösungsstrategien zwischen den beiden Problemen übertragbar
sind. Vor allem läßt sich damit die Differentialgleichung der geodätischen Linie
in kanonischer Form angeben.
als unabhängigem Parameter.
Dies führt dazu, daß Lösungsstrategien zwischen den beiden Problemen übertragbar
sind. Vor allem läßt sich damit die Differentialgleichung der geodätischen Linie
in kanonischer Form angeben.
Aufgrund der zuvor beschriebenen Analogie, ist es möglich, den Hamiltonformalismus
zur Lösung der geodätischen Hauptaufgaben zu verwenden. Angewandt auf die Problematik
der geodätischen Hauptaufgaben auf einem Rotationsellipsoid, folgt aus (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
und wenn das Potential den Wert
)
und wenn das Potential den Wert 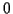 erhält, daß die Gesamtenergie, die
in einem solchen Fall durch die Hamiltonfunktion
erhält, daß die Gesamtenergie, die
in einem solchen Fall durch die Hamiltonfunktion 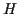 gegeben ist, nur aus
dem Anteil der kinetischen Energie besteht. Wichtig ist hierbei die Betrachtung
des kinematischen Linienelementes
gegeben ist, nur aus
dem Anteil der kinetischen Energie besteht. Wichtig ist hierbei die Betrachtung
des kinematischen Linienelementes
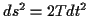 , welches beim Lagrangeformalismus
das geometrische Linienelement ersetzt. Falls nun der Hamiltonformalismus angewandt
werden soll, so muß die quadratische Form für die kinetische Energie durch die
Metrik des Rotationsellipsoides ersetzt werden. Demzufolge ergibt sich analog
zu (
, welches beim Lagrangeformalismus
das geometrische Linienelement ersetzt. Falls nun der Hamiltonformalismus angewandt
werden soll, so muß die quadratische Form für die kinetische Energie durch die
Metrik des Rotationsellipsoides ersetzt werden. Demzufolge ergibt sich analog
zu (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) für die Hamiltonfunktion
) für die Hamiltonfunktion
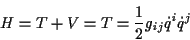 |
(1.45) |
Im Vergleich zum allgemeinen Linienelement
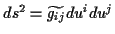 sieht man, daß in der kinetischen Energie und damit auch im kinematischen Linienelement
die Geschwindigkeiten
sieht man, daß in der kinetischen Energie und damit auch im kinematischen Linienelement
die Geschwindigkeiten
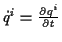 auftreten.
Bei der Allgemeinen Darstellung sind jedoch nur die Differentiale
auftreten.
Bei der Allgemeinen Darstellung sind jedoch nur die Differentiale 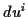 vorhanden. Aus diesem Grund ergibt sich die Hamiltonfunktion zur Bestimmung
der kürzesten Verbindung zweier Punkte in beliebigen Riemannschen Räumen zu
vorhanden. Aus diesem Grund ergibt sich die Hamiltonfunktion zur Bestimmung
der kürzesten Verbindung zweier Punkte in beliebigen Riemannschen Räumen zu
Um das Problem lösen zu können, müssen die generalisierten Geschwindigkeiten
in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) eliminiert werden, damit sich die
Hamiltonfunktion in der benötigten Form ergibt. Dabei kann man die Bestimmungsgleichung
für die generalisierten Impulse
) eliminiert werden, damit sich die
Hamiltonfunktion in der benötigten Form ergibt. Dabei kann man die Bestimmungsgleichung
für die generalisierten Impulse
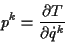 |
(1.46) |
verwenden.
Für den Fall der Lösung der geodätischen Hauptaufgaben folgt mit (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
und
)
und
die Hamiltonfunktion
oder für ein allgemeines orthogonales Flächenparametersystem
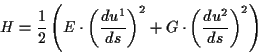 |
(1.47) |
Unter Verwendung von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) für den
Fall eines Potentials
) für den
Fall eines Potentials 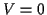 , d.h. es gilt
, d.h. es gilt 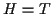 , ergeben sich die
Bestimmungsgleichungen für die 'generalisierten Impulse'
, ergeben sich die
Bestimmungsgleichungen für die 'generalisierten Impulse'
Einsetzen der quadrierten Impulse in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) führt
zur Hamiltonfunktion des Systems, die dann im Falle der geodätischen Hauptaufgaben
auf einem Rotationsellipsoid folgende Form annimmt
) führt
zur Hamiltonfunktion des Systems, die dann im Falle der geodätischen Hauptaufgaben
auf einem Rotationsellipsoid folgende Form annimmt
Die kanonischen Gleichungen lauten dann
sowie
Auf einfache Weise lösen läßt sich das Problem, wenn man die Erzeugende einer
Transformation findet, für die die neuen Koordinaten zyklisch werden. Diese
muß dann (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) erfüllen, wobei die Separation
der Variablen zur gesuchten Lösung für die Erzeugende führt (es ergeben sich
elliptische Funktionen). Aus den konstanten neuen 'Impulsen' und Koordinaten
lassen sich über die Transfomationsformeln
) erfüllen, wobei die Separation
der Variablen zur gesuchten Lösung für die Erzeugende führt (es ergeben sich
elliptische Funktionen). Aus den konstanten neuen 'Impulsen' und Koordinaten
lassen sich über die Transfomationsformeln
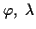 sowie
sowie
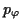 und
und 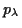 in Abhängigkeit von
in Abhängigkeit von 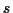 berechnen,
so daß damit das Problem gelöst ist.
berechnen,
so daß damit das Problem gelöst ist.
An dieser Stelle sei noch auf zwei weitere Ansätze zur Lösung der geodätischen
Hauptaufgaben über die kanonische Darstellung der geodätischen Linie verwiesen.
Der Ansatz von SCHÜRER (1975) geht im Unterschied zum zuvor dargelegten, von
der reduzierten Breite 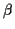 mit
mit
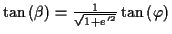 aus, was an (
aus, was an (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) nichts ändert. Der Metriktensor
hat dann die etwas einfachere Form
) nichts ändert. Der Metriktensor
hat dann die etwas einfachere Form
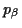 und
und 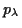 werden entsprechend dem obigen Ansatz
eingeführt, jedoch umgeht er die Lösung der elliptischen Funktionen, indem er
die Hamiltonfunktion in zwei Anteile zerlegt. Die Unterteilung erfolgt derart,
daß die erste Teilfunktion
werden entsprechend dem obigen Ansatz
eingeführt, jedoch umgeht er die Lösung der elliptischen Funktionen, indem er
die Hamiltonfunktion in zwei Anteile zerlegt. Die Unterteilung erfolgt derart,
daß die erste Teilfunktion 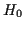 ohne Probleme mit dem Hamiltonformalismus
gelöst und die Restfunktion
ohne Probleme mit dem Hamiltonformalismus
gelöst und die Restfunktion 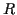 als Störfunktion in Analogie zur Störungsrechnung
in der Himmelsmechanik betrachtet werden kann. Die Lösung von (
als Störfunktion in Analogie zur Störungsrechnung
in der Himmelsmechanik betrachtet werden kann. Die Lösung von (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
mit
)
mit 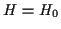 führt zur 'Bewegungsgleichung' der geodätischen
Linie auf einer Kugelfläche. Die hier abgeleiteten Formeln eignen sich gut zur
Untersuchung des Verlaufs der geodätischen Linien über mehrere Umläufe hinweg.
führt zur 'Bewegungsgleichung' der geodätischen
Linie auf einer Kugelfläche. Die hier abgeleiteten Formeln eignen sich gut zur
Untersuchung des Verlaufs der geodätischen Linien über mehrere Umläufe hinweg.
Einen weitere Lösung kann KLOTZ (1991) entnommen werden. Er gelangt über den
Hamiltonformalismus zu einer integralen Darstellung der ellipsoidischen Länge
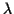 in Abhängigkeit der von reduzierten Breite
in Abhängigkeit der von reduzierten Breite 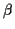 .
.
Im Rahmen dieses zweiten Teils der Arbeit wurde mit MATLAB unter WINDOWS ein
Programmsystem erstellt, das dem Benutzer die Möglichkeit bietet numerische
und geometrische Eigenschaften von geodätischen Linien auf einem Rotationsellipsoid
zu untersuchen. Hierbei wurde für die Berechnung der geodätischen Hauptaufgaben
auf die numerische Integration eines Differentialgleichungssystems der geodätischen
Linie in kartesischen Koordinaten zurückgegriffen. Um die geometrischen Eigenschaften
von geodätischen Linien zu untersuchen, ist es notwendig ihren Verlauf auf der
Bezugsfläche graphisch zu visualisieren. Das erstellte Programmsystem bietet
hierzu die Möglichkeit, nach der Berechnung der geodätischen Hauptaufgaben,
den Verlauf der zugehörigen Geodäte auf der Bezugsfläche, stellvertretend durch
eine frei zu wählende Zahl von Stützstellen, dreidimensional darzustellen. Der
Blickpunkt kann beliebig gewählt werden und es besteht die Möglichkeit einer
Vergrösserung bzw. Verkleinerung. Für die Aufgaben der Landesvermessung ist
es nötig, die geodätischen Hauptaufgaben unter Vorgabe einer bestimmten Fehlerschranke
zu lösen. In den meisten numerischen Ansätzen geschieht dies durch eine Fehlerschätzung.
In dieser Arbeit wird jedoch ein anderer Weg beschritten. Es wird eine, speziell
auf die Lösung der geodätischen Linien auf einem Rotationsellipsoid bezogene
Funktion, mit der die Zahl von Iterationen des Differentialgleichungslösers
nach Vorgabe der geforderten Genauigkeit berechnet werden kann, empirisch abgeleitet.
Als ein Beispiel für die Untersuchung numerischer Eigenschaften der Geodäten
auf einem Rotationsellipsoid bietet das Programmsystem weiterhin die Möglichkeit
ein geodätisches Parallelkoordinatensystem in Soldnerscher Anordnung zu berechnen
und darzustellen.
Allgemein ist eine Differentialgleichung erster Ordnung gegeben durch
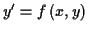 ,
die Werte
,
die Werte 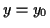 sowie
sowie 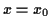 seien als bekannt vorausgesetzt.
Das Problem besteht nun darin, den Funktionswert der Funktion
seien als bekannt vorausgesetzt.
Das Problem besteht nun darin, den Funktionswert der Funktion
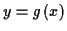 an der Stelle
an der Stelle 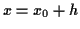 zu bestimmen. Im weiteren sei dieser mit
zu bestimmen. Im weiteren sei dieser mit 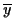 bezeichnet. Die zugehörige Integralgleichung lautet damit
bezeichnet. Die zugehörige Integralgleichung lautet damit
.
Eine Möglichkeit der Lösung besteht darin, die Funktion
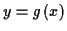 an der Stelle
an der Stelle 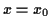 in eine Taylorreihe
in eine Taylorreihe
zu entwickeln. Mit der Ausgangsgleichung gilt
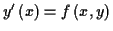 und für die höheren Ableitungen folgt
und für die höheren Ableitungen folgt
Wenn man nun die partiellen Ableitungen durch
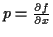 ,
,
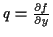 ,
,
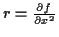 ,
,
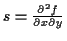 ,
,
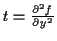 ersetzt, so erhält man den folgenden übersichtlichen Ausdruck für die Taylorentwicklung
an der Stelle
ersetzt, so erhält man den folgenden übersichtlichen Ausdruck für die Taylorentwicklung
an der Stelle 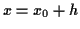 :
:
Für Approximationszwecke ist es ausreichend die ersten beiden Glieder der Taylorentwicklung
zu betrachten. Wenn man das Integrationsintervall h in infinitisimal kleine
Teilintervalle der Breite 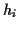 ,
, 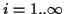 unterteilt, so kann
man auf diese Weise den Funktionswert der Funktion
unterteilt, so kann
man auf diese Weise den Funktionswert der Funktion
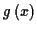 an der Stelle
an der Stelle 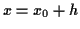 iterativ bestimmen. Der Rechenaufwand kann durch
Berücksichtigung höherer Glieder der Taylorentwicklung zwar verringert werden,
jedoch erhöht sich dabei die Komplexität der Funktionen.
iterativ bestimmen. Der Rechenaufwand kann durch
Berücksichtigung höherer Glieder der Taylorentwicklung zwar verringert werden,
jedoch erhöht sich dabei die Komplexität der Funktionen.
Eine andere Alternative ergibt sich, wenn angenommen wird, daß bspw. die Werte
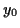 ,
, 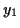 ,
, 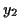 der Funktion
der Funktion
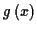 an den Stellen
an den Stellen 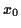 ,
,
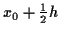 und
und 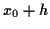 vorliegen.
Mit diesen Werten folgt mit der Prismaregel2.1 :
vorliegen.
Mit diesen Werten folgt mit der Prismaregel2.1 :
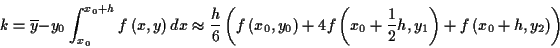 |
(2.1) |
Die in Wirklichkeit, bis auf 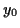 , unbekannten Funktionswerte von
, unbekannten Funktionswerte von
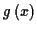 ,
werden mittels einer nach Runge bezeichneten Methode wie folgt approximiert:
,
werden mittels einer nach Runge bezeichneten Methode wie folgt approximiert:
Eingesetzt in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ), die genäherte Gleichung für
), die genäherte Gleichung für 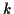 , ergibt
sich dann
, ergibt
sich dann
Hierbei wird 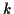 iterativ über
iterativ über
mit
bestimmt. Je nach Zahl und Wahl der Approximationen für 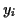 , kann das
Verfahren abgeändert werden. Die Abbildung
, kann das
Verfahren abgeändert werden. Die Abbildung ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) gibt das Prinzip des
Verfahrens nach Runge wieder.
gibt das Prinzip des
Verfahrens nach Runge wieder.
Abbildung:
Prinzip des Verfahrens nach Runge
|
|
Wie leicht zu erkennen ist, läßt sich dieses Verfahren allgemeiner darstellen
mit
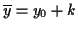 , wobei sich
, wobei sich  als eine Funktion der Integrationsweite
als eine Funktion der Integrationsweite
 und einer diskreten Näherungsfunktion, die im weiteren mit
und einer diskreten Näherungsfunktion, die im weiteren mit  bezeichnet wird, darstellen läßt . Für
bezeichnet wird, darstellen läßt . Für 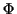 2.2 gilt:
2.2 gilt:
Es werden dabei von 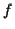 und
und 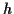 unabhängige Zahlen
unabhängige Zahlen 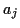 ,
, 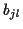 ,
,
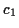 ,
,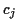 mit
mit 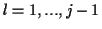 und
und 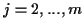 unter
der Voraussetzung der Bedingungen
unter
der Voraussetzung der Bedingungen
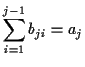 und
und
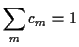 so bestimmt, daß die Beziehungen
so bestimmt, daß die Beziehungen
für  und
und
eine möglichst hohe Konsistenzordnung ergeben. Da diese Näherung über die Approximation
der Funktionswerte 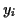 nicht zu einer exakten Lösung führen kann, wird
das Integrationsintervall, wie bereits bei der Integration über Reihenentwicklung
erwähnt, in Teilintervalle
nicht zu einer exakten Lösung führen kann, wird
das Integrationsintervall, wie bereits bei der Integration über Reihenentwicklung
erwähnt, in Teilintervalle 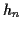 eingeteilt. Auf diesem Weg erhält man
das Ergebnis über
eingeteilt. Auf diesem Weg erhält man
das Ergebnis über
für
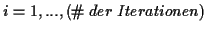 .
.
Das Verfahren wird auf Systeme von Differentialgleichungen übertragen, indem
man für die Koeffizienten 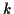 eine Matrix ansetzt, in der für jede Gleichung
des Systems eine Spalte sukzessive in den Iterationsschritten bestimmt wird.
eine Matrix ansetzt, in der für jede Gleichung
des Systems eine Spalte sukzessive in den Iterationsschritten bestimmt wird.
Für die Realisierung unter MATLAB 5.0 wird, wegen des benötigten Zugriffs auf
algebraische Objekte die symbolische Toolbox von MATLAB verwandt. Diese beruht
auf einem MAPLE Kern und ermöglicht es, das Programm als Funktion zu realisieren,
welche symbolische Vektoren als Eingabewerte verarbeiten kann. Die Berechnung
erfolgt nach dem im vorigen Abschnitt beschriebenen Verfahren, wobei die Zahl
der Iterationen vorgegeben werden muß, da keine automatische Schrittweitensteuerung
implementiert wurde. Der Aufruf der Funktion (Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt ein Flußdiagramm) von der MATLAB Eingabeaufforderung geschieht über:
zeigt ein Flußdiagramm) von der MATLAB Eingabeaufforderung geschieht über:
z=RK7multi(DGLSYS,i,h,Naeherung,x0);
Abbildung:
Flußdiagramm der Funktion RK7multi.m
|
|
Dabei bezeichnet DGLSYS einen symbolischen Spaltenvektor der Form sym('[y1;y2;...;yn]'),
der die rechten Seiten der Differentialgleichungen enthält. Die Variable i
steht für die Zahl der Iterationen, h bezeichnet die Integrationsweite,
Y ist der symbolische Vektor der Variablennamen in der Form sym('[Y1;Y2;...;Yn]'),
Naeherung ist ein Zeilenvektor mit den bekannten Werten der Variablen
an den Näherungstellen und x0 bezeichnet den Startwert der unabhängigen
Variabeln 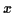 .
.
Beispiel: Es sei folgendes Differentialgleichungssytem erster
Ordnung gegeben:
Für dieses sind 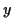 und
und 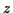 an der Stelle
an der Stelle 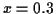 , für diejenige
partikuläre Lösung zu prädizieren, für die gilt
, für diejenige
partikuläre Lösung zu prädizieren, für die gilt
und
Der Funktionsaufruf lautet dann:
z=RK7multi(sym('[x+sqrt(z);y-sqrt(z)]'),1,0.1,sym('[y;z]'),[0.5,0],0.2);
(für i kann hier 1 angesetzt werden) Es ergibt sich
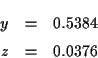
ARINGER (1994) beschreibt die Möglichkeit der Lösung der geodätischen Hauptaufgaben
über eine Darstellung der Differentialgleichungen der geodätischen Linie in
kartesischen Koordinaten. Der Grund für deren Einführung liegt in den Problemen,
die sich aufgrund von Singularitäten bei der Parameterdarstellung regulärer
Flächen ergeben. Werden beispielsweise geographische Breite und geographische
Länge als Parameter zur Darstellung einer Einheitskugel verwendet, so ergeben
sich diese in den Polen. Eine andere Möglichkeit bietet die Wahl von Mongeschen
Flächenstücken, wobei hier Fallunterscheidungen zu treffen sind, da sonst Singularitäten
an den begrenzenden Großkreisen auftreten können. Diese Problematiken lassen
sich ebenfalls auf das Ellipsoid übertragen. Dort kommt es dann in der Nähe
der Unstetigkeitsstellen zu numerischen Unsicherheiten bei der Berechnung der
geodätischen Hauptaufgaben über Quadraturverfahren. Als Lösung schlägt ARINGER
die Wahl der impliziten Form
der Flächendarstellung in kartesischen Koordinaten vor. Über die Bestimmungsgleichung
der geodätischen Linie
mit der Normalkrümmung
und dem zugehörigen Normalenvektor
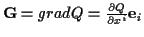 ,
wobei
,
wobei
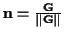 ,
leitet er das folgende Differentialgleichungssystem her:
,
leitet er das folgende Differentialgleichungssystem her:
![\begin{displaymath}
\left[ \begin{array}{c}
DY_{1}=Y_{2}\\
DY_{2}=\frac{-Y_{1}}...
...}^{2}+\frac{a^{2}}{b^{2}}Y_{6}^{2}\right)
\end{array}\right]
\end{displaymath}](img497.gif) |
(2.2) |
Die Differentiale sind mit  , die Variablen mit
, die Variablen mit 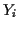 bezeichnet.
bezeichnet.
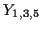 stehen hierbei für die kartesischen Koordinaten des Anfangspunktes,
die drei übrigen Variablen bezeichnen die Komponenten des Tangenteneinheitsvektors
im Anfangspunkt, die zunächst über die gegebenen Größen zu berechnen sind. Wie
bereits erwähnt, besitzt die implizite Art der Flächendarstellung und damit
das aus dieser abgeleitete Differentialgleichungssystem, den Vorteil, daß es
frei von Singularitäten ist. Den meisten Verfahren, die bei der numerischen
Integration der ersten Hauptaufgabe Verwendung finden, liegt das, in der Literatur
meist angegebene, Gleichungssystem
stehen hierbei für die kartesischen Koordinaten des Anfangspunktes,
die drei übrigen Variablen bezeichnen die Komponenten des Tangenteneinheitsvektors
im Anfangspunkt, die zunächst über die gegebenen Größen zu berechnen sind. Wie
bereits erwähnt, besitzt die implizite Art der Flächendarstellung und damit
das aus dieser abgeleitete Differentialgleichungssystem, den Vorteil, daß es
frei von Singularitäten ist. Den meisten Verfahren, die bei der numerischen
Integration der ersten Hauptaufgabe Verwendung finden, liegt das, in der Literatur
meist angegebene, Gleichungssystem
![\begin{displaymath}
\left[ \begin{array}{c}
\frac{\partial u}{\partial s}=\frac{...
...}\sqrt{g_{11}}}\sin \left( \alpha \right)
\end{array}\right]
\end{displaymath}](img501.gif) |
(2.3) |
zugrunde. Für das Linienelement in ellipsoidischen Koordinaten gilt
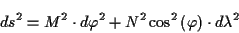 |
(2.4) |
mit dem Meridiankrümmungshalbmesser
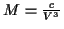 und dem Querkrümmungshalbmesser
und dem Querkrümmungshalbmesser
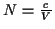 .
.
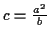 bezeichnet den Polkrümmungshalbmesser
und es gilt
bezeichnet den Polkrümmungshalbmesser
und es gilt
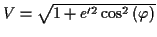 , mit der
zweiten numerischen Exzentrizität
, mit der
zweiten numerischen Exzentrizität
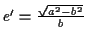 . Für
den kovarianten Metriktensor folgt dementsprechend
. Für
den kovarianten Metriktensor folgt dementsprechend
Eingesetzt in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergibt sich folgendes Differentialgleichungssystem
erster Ordnung für die geodätische Linie auf dem Rotationsellipsoid:
) ergibt sich folgendes Differentialgleichungssystem
erster Ordnung für die geodätische Linie auf dem Rotationsellipsoid:
![\begin{displaymath}
\left[ \begin{array}{c}
\frac{\partial \varphi }{\partial s}...
...varphi \right) \sin \left( \alpha \right)
\end{array}\right]
\end{displaymath}](img509.gif) |
(2.5) |
Dieses Gleichungssystem kann zur Lösung der 1. geodätischen Hauptaufgabe direkt
integriert werden, wobei hier jedoch auf die schon erwähnten Singularitäten
in den Polen, hervorgerufen durch die Wahl der ellipsoidischen Koordinaten,
zu achten ist.
Mit MATLAB wurde eine graphische Benutzerschnittstelle entwickelt, die die Berechnung
der 1. geodätischen Hauptaufgabe in kartesischen Koordinaten auf einem vorgegebenen
Rotationsellipsoid ermöglicht. Dabei wird zur Lösung des Gleichungssystems (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
über eine Anfangswertaufgabe auf die zuvor eingeführte Funktion RK7multi
zurückgegriffen. Der Funktionsaufruf lautet in diesem Fall:
)
über eine Anfangswertaufgabe auf die zuvor eingeführte Funktion RK7multi
zurückgegriffen. Der Funktionsaufruf lautet in diesem Fall:
z=RK7multi(DGLSYS,schritte,s,Y,[x1 t(1) x2 t(2) x3 t(3)],0);
mit den Variablen
- DGLSYS: Symbolische Zeilenmatrix mit den rechten Seiten der Differentialgleichungen
(
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ). (kann dem Quelltext entnommen werden)
). (kann dem Quelltext entnommen werden)
- Y=sym('[y1;y2;y3;y4;y5;y6]');
- schritte bezeichnet die vorzugebende Zahl der Iterationen
- s entspricht dem Integrationsintervall
- [x1 t(1) x2 t(2) x3 t(3)] gibt die Komponenten des Anfangsvektors
und des Tangentenvektors im Anfangspunkt an
Es sei hier zu bemerken, daß in DGLSYS die Konstantenbezeichner vor
Aufruf der Funktion noch durch ihre numerischen Werte zu ersetzen sind. Die
in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) dargestellte Benutzerschnittstelle (G(raphical)U(ser)I(nterface))
kann durch Aufruf der Funktion guiawp_graphik.m an der MATLAB Eingabeaufforderung
gestartet werden.
dargestellte Benutzerschnittstelle (G(raphical)U(ser)I(nterface))
kann durch Aufruf der Funktion guiawp_graphik.m an der MATLAB Eingabeaufforderung
gestartet werden.
Abbildung:
GUI für Lösung des Anfangswertproblems
|
|
Die Felder für die Anfangswerte und die vorzugebenden Ellipsoidparameter lassen
sich editieren, und die Funktion geo_haupt_1.m, welche die Übergabe
der Daten zwischen dem GUI und dem Script RKF7multi.m übernimmt,
wird über den Button 'Berechnung Starten' aufgerufen. Das Programm
selbst bietet zum einen die Möglichkeit eine konstante Zahl von Iterationen
vorzugeben, zum anderen kann aus verschiedenen Genauigkeiten ausgewählt werden.
Mit der Ableitung, des für diese Aufgabe empirisch zu bestimmenden Zusammenhangs
zwischen Genauigkeit und vorzugebender Zahl der Iterationen, beschäftigt sich
der folgende Abschnitt. Hier sei zu erwähnen, daß man durch Wahl des Schalters
'Genauigkeit auswählen' unter 9 verschiedenen Genauigkeiten der Lösung
der Anfangswertaufgabe wählen kann, und mit Übernahme dieser Wahl, die Zahl
der benötigten Iterationen automatisch, nach Auswerten der Iterationsfunktion,
in die Oberfläche übernommen werden. Auf die Bedeutung der rechts im Fenster
angeordneten Schalter 'Ephemeridenberechnung' und 'Zurück zur
Hauptauswahl' wird in den folgenden Abschnitte noch eingegangen. Die Rechenzeit2.3 des Programms (0.1''-2''/AWP) liegt in der Regel beim 2- bis 9- fachen eines
kompilierten FORTRAN-Programms.
Abbildung:
Rechenzeit in Abhängigkeit von der Entfernung
|
|
Verkürzen läßt sich diese, indem man entweder vorhandene FORTRAN- bzw. C-Funktionen
über ein API (Application Program Interface)
in die MATLAB-Routinen einbindet oder einen MATLAB-Compiler wie MATCOM oder
MIDEVA2.4 benutzt, der die m-Scripte in C++ übersetzt und dann compiliert.
Da bei der Realisierung des Programms auf eine automatische Schrittweitensteuerung2.5 verzichtet wurde, ist es wichtig, die für eine vorgegebene Genauigkeit der
Endpunktkoordinaten nötige Schrittweite, bzw. die Zahl der Iterationen in Abhängigkeit
der Integrationsweite des Runge-Kutta-Verfahrens, empirisch abzuleiten. Über
ein Hilfsprogramms wird dabei die Zahl der Iterationen solange erhöht, bis sich
die Endpunktkoordinaten der Lösung mit 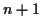 Iterationen von denen der
Lösung mit
Iterationen von denen der
Lösung mit 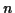 Iterationen nur noch um eine vorgegebene Schranke
Iterationen nur noch um eine vorgegebene Schranke 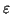 unterscheiden. Setzt man beispielsweise als Schranke für die Genauigkeit der
kartesischen Koordinaten der Endpunkte einen Wert von
unterscheiden. Setzt man beispielsweise als Schranke für die Genauigkeit der
kartesischen Koordinaten der Endpunkte einen Wert von
 an, so ergibt der in Abb.
an, so ergibt der in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) dargestellte, wie zu erwarten
lineare, Zusammenhang zwischen der Anzahl der benötigten Iterationen und der
Länge der geodätischen Linie.
dargestellte, wie zu erwarten
lineare, Zusammenhang zwischen der Anzahl der benötigten Iterationen und der
Länge der geodätischen Linie.
Abbildung:
Iterationen in Abhängigkeit von der Integrationsweite
s
|
|
Im weiteren bestehen Abhängigkeiten der nötigen Iterationen von der Abplattung,
dem Azimut sowie von der geforderten Genauigkeit 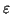 . In den
oberen beiden Graphen der Abb.
. In den
oberen beiden Graphen der Abb.![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) 2.6 ist gut zu erkennen, daß der Einfluß der Abplattung auf die Iterationen bei
Integration in Polrichtung am stärksten ist, wohingegen bei Integration in Äquatorrichtung
diese Abhängigkeit nicht mehr auftritt. Dies war von vornherein klar, da mit
geringerem Azimut die Abweichung der geodätischen Linie von einem ebenen Kreisabschnitt
immer größer wird. In Äquatorrichtung entspricht die geodätische Linie dann
dem Äquator. Aufgrund der Tatsache, daß die maximale Zahl der benötigten Iterationen
in Polrichtung auftritt, wird bei der weiteren Ableitung einer Näherungsfunktion
immer von dieser Integrationsrichtung ausgegangen und somit der Einfluß des
Azimuts unter Inkaufnahme längerer Rechenzeiten unberücksichtigt gelassen. Die
beiden unteren Graphen zeigen zum einen den Einfluß der Abplattung auf die Funktion
2.6 ist gut zu erkennen, daß der Einfluß der Abplattung auf die Iterationen bei
Integration in Polrichtung am stärksten ist, wohingegen bei Integration in Äquatorrichtung
diese Abhängigkeit nicht mehr auftritt. Dies war von vornherein klar, da mit
geringerem Azimut die Abweichung der geodätischen Linie von einem ebenen Kreisabschnitt
immer größer wird. In Äquatorrichtung entspricht die geodätische Linie dann
dem Äquator. Aufgrund der Tatsache, daß die maximale Zahl der benötigten Iterationen
in Polrichtung auftritt, wird bei der weiteren Ableitung einer Näherungsfunktion
immer von dieser Integrationsrichtung ausgegangen und somit der Einfluß des
Azimuts unter Inkaufnahme längerer Rechenzeiten unberücksichtigt gelassen. Die
beiden unteren Graphen zeigen zum einen den Einfluß der Abplattung auf die Funktion
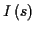 , die im weiteren die Abhängigkeit der nötigen Iterationen
von der Integrationsweite
, die im weiteren die Abhängigkeit der nötigen Iterationen
von der Integrationsweite 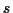 beschreibt, sowie den Einfluß einer variierenden
Integrationsweite auf die Funktion
beschreibt, sowie den Einfluß einer variierenden
Integrationsweite auf die Funktion
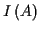 , durch die der Zusammenhang
zwischen den Iterationen und dem Azimut
, durch die der Zusammenhang
zwischen den Iterationen und dem Azimut 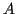 erfaßt wird.
erfaßt wird.
Abbildung:
Abhängigkeiten von Azimut und Abplattung
|
|
Der nächste Schritt besteht darin die Einflüsse der übrigen 3 Parameter, Integrationsweite
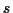 , Abplattung
, Abplattung 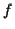 und geforderte Genauigkeit
und geforderte Genauigkeit 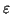 in einer Funktion
in einer Funktion
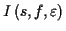 zusammenzufassen.
Es bietet sich dabei an, die Einflüsse von
zusammenzufassen.
Es bietet sich dabei an, die Einflüsse von 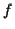 und
und 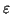 auf den in Abb.
auf den in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) dargestellten linearen Zusammenhang
dargestellten linearen Zusammenhang
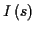 zu untersuchen. Im ersten Graphen von Abb.
zu untersuchen. Im ersten Graphen von Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) sind zunächst verschiedene
sind zunächst verschiedene
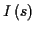 Kurven für unterschiedliche
Abplattungswerte
Kurven für unterschiedliche
Abplattungswerte 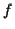 in
in
![\( \left[ \%\right] \)](img520.gif) dargestellt. Darunter
folgt derselbe Graph für variierende
dargestellt. Darunter
folgt derselbe Graph für variierende 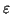 (
(
 ). Aus diesen beiden Abbildungen folgt, daß die Einflüsse der anderen beiden
Parameter auf
). Aus diesen beiden Abbildungen folgt, daß die Einflüsse der anderen beiden
Parameter auf
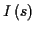 nichts an deren linearer Eigenschaft
ändern. Im weiteren sind daher die Veränderungen der Parameter
nichts an deren linearer Eigenschaft
ändern. Im weiteren sind daher die Veränderungen der Parameter
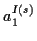 und
und
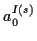 des Polynoms erster Ordnung
des Polynoms erster Ordnung
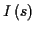 bei Änderung von
bei Änderung von 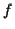 und
und 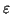 zu untersuchen. Für
die Abhängigkeit der Steigung
zu untersuchen. Für
die Abhängigkeit der Steigung
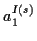 der Geraden
der Geraden
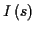 von der geforderten Genauigkeit
von der geforderten Genauigkeit 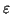 (vgl. Abb.
(vgl. Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ),
ergibt sich, nach Ermittlung der
),
ergibt sich, nach Ermittlung der
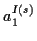 über lineare
Regression, der folgende logarithmische Zusammenhang :
über lineare
Regression, der folgende logarithmische Zusammenhang :
Die Abhängigkeit des y-Achsenabschnittes der
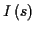 Kurven
kann dem 2. Graphen in Abb.
Kurven
kann dem 2. Graphen in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) entnommen werden. Im Folgenden
sei die Änderung von
entnommen werden. Im Folgenden
sei die Änderung von
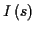 bei Variation von
bei Variation von 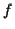 , unter
Festhalten von
, unter
Festhalten von 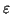 , mit
, mit
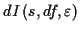 bezeichnet.
bezeichnet.
Abbildung:
Lineare Zusammenhänge zwischen
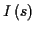 und
und 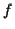 sowie
sowie
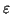
|
|
Der Koeffizient
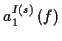 läßt sich durch
ein Polynom dritten Grades in
läßt sich durch
ein Polynom dritten Grades in 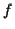 approximieren:
approximieren:
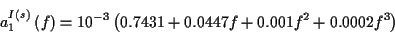 |
(2.6) |
Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt nun, analog zu Abb.
zeigt nun, analog zu Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ,
die sich für diesen Fall ergebenden Graphen.
,
die sich für diesen Fall ergebenden Graphen.
Abbildung:
Änderung der Parameter von
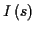 in Abhängigkeit von
in Abhängigkeit von
|
|
Abbildung:
Änderung der Parameter von
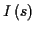 in Abhängigkeit von
in Abhängigkeit von 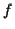
|
|
Man kann zur Ableitung der Funktion
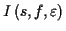 2 Wege beschreiten, zum einen kann
2 Wege beschreiten, zum einen kann
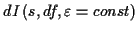 unter Variation von
unter Variation von 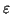 untersucht werden, zum anderen ist der
umgekehrte Weg möglich. Aufgrund der Einfachheit der Polynome 3. Grades wird
der erste Weg beschritten, und 4 Funktionen, welche mit
untersucht werden, zum anderen ist der
umgekehrte Weg möglich. Aufgrund der Einfachheit der Polynome 3. Grades wird
der erste Weg beschritten, und 4 Funktionen, welche mit
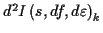 für
für  bezeichnet werden, lassen sich aus den Variationen der in
(
bezeichnet werden, lassen sich aus den Variationen der in
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) eingeführten Koeffizienten des Polynoms unter Änderung von
) eingeführten Koeffizienten des Polynoms unter Änderung von
 ableiten.
ableiten.
Abbildung:
Steigungs- und y-Achsenabschnittsfunktion
in Abhängigkeit von der zu fordernden Genauigkeit
|
|
In Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) sind wiederum analog zu
Abb.
sind wiederum analog zu
Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) die sich ergebenden Steigungsfunktionen sowie die
y-Achsenabschnittsverläufe für verschiedene
die sich ergebenden Steigungsfunktionen sowie die
y-Achsenabschnittsverläufe für verschiedene  dargestellt.
Die daraus folgenden Koeffizienten der angesetzten Polynome können der Tabelle
dargestellt.
Die daraus folgenden Koeffizienten der angesetzten Polynome können der Tabelle
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) entnommen werden.
entnommen werden.
Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt eine graphische Darstellung der
zeigt eine graphische Darstellung der
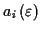 aus Tabelle
aus Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) .
Wie man dieser entnehmen kann, lohnt es aufgrund der Sprünge nicht, die sich
ergebenden Zusammenhänge funktional zu approximieren.
.
Wie man dieser entnehmen kann, lohnt es aufgrund der Sprünge nicht, die sich
ergebenden Zusammenhänge funktional zu approximieren.
Abbildung:
Darstellung der Approximationspolynome
|
|
Die im Programm implementierte Iterationsfunktion wird folglich für die diskreten
Werte 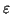 , wie sie der Tabelle
, wie sie der Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zu entnehmen sind, bestimmt. Die Möglichkeit der Wahl der Genauigkeit zwischen
zu entnehmen sind, bestimmt. Die Möglichkeit der Wahl der Genauigkeit zwischen
![\( 0.5[mm] \)](img551.gif) und
und ![\( 50[km] \)](img552.gif) reicht für die Anwendung des Programms vollkommen
aus.
reicht für die Anwendung des Programms vollkommen
aus.
Nach diesen Ergebnissen der Untersuchung der Iterationsfunktion erfolgt die
automatische Berechnung der, für eine vorgegebene Genauigkeit benötigten, Zahl
der Iterationen des Differentialgleichungslösers, indem zunächst mit dem zu
erreichenden Genauigkeitswert aus Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) die
zugehörigen Polynomkoeffizienten bestimmt, dann der Funktionswert dieses Polynoms
an der Stelle der gegebenen Abplattung ermittelt und mit diesem die Funktion
die
zugehörigen Polynomkoeffizienten bestimmt, dann der Funktionswert dieses Polynoms
an der Stelle der gegebenen Abplattung ermittelt und mit diesem die Funktion
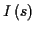 ausgewertet wird. Wie aus Abb.
ausgewertet wird. Wie aus Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) unten ersichtlich, ist es angebracht den y-Achsenabschnitt, der scheinbar keinem
funktionalen Zusammenhang folgt ,als Konstante mit dem Wert
unten ersichtlich, ist es angebracht den y-Achsenabschnitt, der scheinbar keinem
funktionalen Zusammenhang folgt ,als Konstante mit dem Wert 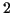 einzuführen.
Damit ergibt sich folgende Iterationsfunktion:
einzuführen.
Damit ergibt sich folgende Iterationsfunktion:
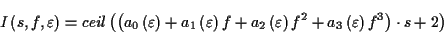 |
(2.7) |
(Diese Funktion wurde ausreichend verprobt.2.7)
Abbildung:
Graphische Darstellung der Polynomkoeffizienten
|
|
Um die Leistungsfähigkeit des Programms zu testen, werden die in ARINGER (1994)
aufgeführten Beispiele berechnet. In Tabelle 8 seiner Dissertation
vergleicht er die Ergebnisse verschiedener Integratoren. Da das hier benutzte
Programm nach dem Runge-Kutta-Verfahren 7. Ordnung arbeitet, werden die Ergebnisse
mit denjenigen verglichen, die ARINGER nach dem, im weiteren mit RKF7
abgekürzten, Runge-Kutta-Fehlberg-Verfahren 7. Ordnung ermittelte. Der Unterschied
der beiden Verfahren liegt in der, beim RKF7 Verwendung findenden Fehlerschätzung2.8 nach FEHLBERG. Bei geod_haupt_1.m ist diese Fehlerschätzung durch
die im vorigen Abschnitt abgeleitete empirische Iterationsfunktion ersetzt worden,
so daß das Ergebnis ebenfalls nach Vorgabe einer gewünschten Genauigkeit ermittelt
werden kann2.9. in Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) sind nun die Ergebnisse des RKF72.10 zum Vergleich in der letzten Spalte angeordnet. Bei der Berechnung über
geod_haupt_1.m wurde zunächst die Zahl der Iterationen auf 35 festgelegt.
Die Werte in den Klammern enthalten im Vergleich hierzu die Änderungen, die
sich nach Vorgabe einer Genauigkeit von
sind nun die Ergebnisse des RKF72.10 zum Vergleich in der letzten Spalte angeordnet. Bei der Berechnung über
geod_haupt_1.m wurde zunächst die Zahl der Iterationen auf 35 festgelegt.
Die Werte in den Klammern enthalten im Vergleich hierzu die Änderungen, die
sich nach Vorgabe einer Genauigkeit von
![\( \varepsilon =0.0005\left[ m\right] \)](img564.gif) über die Auswertung der empirischen Iterationsfunktion zeigten. Die Zahl der
sich für diese Genauigkeit nach (
über die Auswertung der empirischen Iterationsfunktion zeigten. Die Zahl der
sich für diese Genauigkeit nach (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) ergebenden nötigen
Iterationen ist zusätzlich angegeben. Der Tabelle kann entnommen werden, daß
die Ergebnisse für die Koordinaten sich bei Längen bis zu
) ergebenden nötigen
Iterationen ist zusätzlich angegeben. Der Tabelle kann entnommen werden, daß
die Ergebnisse für die Koordinaten sich bei Längen bis zu 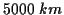 nicht
unterscheiden. Werden die Entfernungen jedoch größer treten hier Abweichungen
im Bereich einiger zehntel Millimeter auf. Der Azimut im Endpunkt wird nur für
nicht
unterscheiden. Werden die Entfernungen jedoch größer treten hier Abweichungen
im Bereich einiger zehntel Millimeter auf. Der Azimut im Endpunkt wird nur für
 identisch erhalten. Für
identisch erhalten. Für 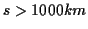 treten Abweichungen
im Bereich von
treten Abweichungen
im Bereich von 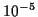 Sekunden auf. Da Abweichungen in dieser Größenordnung
auch bei Aringers Vergleich der verschiedenen Integratoren vorkommen2.11, ist es schwierig auf deren Ursache zu schließen. Ein möglicher Grund könnte
in der unterschiedlichen Größenordnung der Anfangswerte liegen, die jedoch durch
eine Änderung der Skalierung umgangen werden kann.
Sekunden auf. Da Abweichungen in dieser Größenordnung
auch bei Aringers Vergleich der verschiedenen Integratoren vorkommen2.11, ist es schwierig auf deren Ursache zu schließen. Ein möglicher Grund könnte
in der unterschiedlichen Größenordnung der Anfangswerte liegen, die jedoch durch
eine Änderung der Skalierung umgangen werden kann.
Wie im vorigen Abschnitt gezeigt, lassen sich nichtlineare Anfangswertprobleme
auf einfache Weise durch numerische Integration lösen. Bei Randwertaufgaben
ist dies im allgemeinen nicht der Fall, da es sich meist um Probleme mit freiem
Rand, d.h. um Probleme handelt, bei denen das Integrationsintervall nicht vorgegeben,
sondern Teil der Lösung des Randwertproblems ist. Betrachtet man das Gleichungssystem
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) so trifft dies hier ebenfalls zu. Die gesuchte Entfernung
) so trifft dies hier ebenfalls zu. Die gesuchte Entfernung
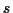 tritt als Integrationsvariable auf. Eine Möglichkeit der Lösung dieses
Problems besteht darin, ein anderes gleichwertiges System aufzustellen, in dem
das Integrationsintervall einer neu einzuführenden unabhängigen Variablen gegeben
ist. ARINGER stellt ein solches System für die Differentialgleichung der geodätischen
Linie in kartesischen Koordinaten in seiner Dissertation2.12 vor.
tritt als Integrationsvariable auf. Eine Möglichkeit der Lösung dieses
Problems besteht darin, ein anderes gleichwertiges System aufzustellen, in dem
das Integrationsintervall einer neu einzuführenden unabhängigen Variablen gegeben
ist. ARINGER stellt ein solches System für die Differentialgleichung der geodätischen
Linie in kartesischen Koordinaten in seiner Dissertation2.12 vor.
Meist werden solche Systeme jedoch nach einem als empirisch zu bezeichnenden
Verfahren, dem s.g. Schießverfahren gelöst. Voraussetzung für dieses
Verfahren sind gute Näherungswerte für die Lösung des Randwertproblems. Im ersten
Schritt wird mit den Näherungswerten eine Anfangswertaufgabe gelöst. Im Fall
der zweiten geodätischen Hauptaufgabe sind die Koordinaten des Anfangs-, sowie
die des Endpunktes gegeben. Man benötigt dann sowohl Näherungswerte für die
Tangentenrichtung an die geodätische Linie im Anfangspunkt, als auch für die
zu bestimmende Entfernung. Nach Berechnung des AWP's können die Sollwerte der
Endpunktkoordinaten mit der Lösung verglichen und eine Abweichung bestimmt werden.2.13 Um das Prinzip mathematisch zu verwirklichen, werden homogene Randbedingungen
der Form
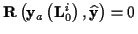 aufgestellt. Hierbei bezeichne
aufgestellt. Hierbei bezeichne
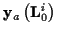 die Lösung der Anfangswertaufgabe mit dem Näherungsvektor
die Lösung der Anfangswertaufgabe mit dem Näherungsvektor
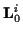 in der
in der 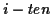 Iteration und
Iteration und
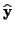 die vorgegebenen
Randwerte für das RWP (geg. Endpunktkoordinaten). Im Falle der zweiten geodätischen
Hauptaufgabe ergeben sich die folgenden Randbedingungen:
die vorgegebenen
Randwerte für das RWP (geg. Endpunktkoordinaten). Im Falle der zweiten geodätischen
Hauptaufgabe ergeben sich die folgenden Randbedingungen:
![\begin{displaymath}
\left[ \begin{array}{c}
R_{1}\\
R_{2}\\
R_{3}\\
R_{4}
\en...
... =\left[ \begin{array}{c}
0\\
0\\
0\\
0
\end{array}\right]
\end{displaymath}](img581.gif) |
(2.8) |
mit
![\( \mathbf{y}_{a}=\left[ \begin{array}{c}
x\\
y\\
z\\
t_{1}\\
t_{2}\\
t_{3}
\end{array}\right] \)](img582.gif) und
und
![\( \widehat{\mathbf{y}}=\left[ \begin{array}{c}
\widehat{x}\\
\widehat{y}\\
\widehat{z}
\end{array}\right] \)](img583.gif)
Als 4. Randbedingung wird der Betrag des Tangenteneinheitsvektors eingeführt.
Damit ist (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) eine nichtlineare Gleichung in
) eine nichtlineare Gleichung in
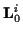 ,
die mit Hilfe des allgemeinen Newtonverfahrens2.14 iterativ gelöst werden kann. Die Bestimmung der Näherungswerte für die
,
die mit Hilfe des allgemeinen Newtonverfahrens2.14 iterativ gelöst werden kann. Die Bestimmung der Näherungswerte für die 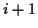 te Iteration erfolgt über:
te Iteration erfolgt über:
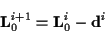 |
(2.9) |
mit den Verbesserungen
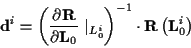 |
(2.10) |
Da die Differentation in (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) nicht explizit durchgeführt
werden kann, muß an dieser Stelle der Differentialquotient durch den Differenzenquotienten
ersetzt werden.
) nicht explizit durchgeführt
werden kann, muß an dieser Stelle der Differentialquotient durch den Differenzenquotienten
ersetzt werden.
Abbildung:
Prinzip des Schießverfahrens
|
|
Im Startvektor
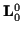 , welcher durch eine geeignete Näherung
zu ermitteln ist, wird die
, welcher durch eine geeignete Näherung
zu ermitteln ist, wird die  -te Komponente um einen noch festzulegenden
Wert
-te Komponente um einen noch festzulegenden
Wert
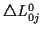 variiert und erneut eine Anfangswertaufgabe
berechnet. Nach der Iteration über
variiert und erneut eine Anfangswertaufgabe
berechnet. Nach der Iteration über  erhält man damit ein lineares Gleichungssystem
für die Ermittlung des Vektors der Verbesserungen
erhält man damit ein lineares Gleichungssystem
für die Ermittlung des Vektors der Verbesserungen
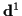 . Die
Startwerte für den
. Die
Startwerte für den  'ten Schritt erhält man über (
'ten Schritt erhält man über (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ).
Nach einer erneuten Berechnung des AWP's kann ein Abbruchkriterium ()
derart eingefügt werden, daß falls die euklidsche Distanz des berechneten Endpunktes
vom Sollwert eine Schranke
).
Nach einer erneuten Berechnung des AWP's kann ein Abbruchkriterium ()
derart eingefügt werden, daß falls die euklidsche Distanz des berechneten Endpunktes
vom Sollwert eine Schranke 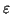 unterschreitet, das Schießverfahren
beendet wird. Die Abb.
unterschreitet, das Schießverfahren
beendet wird. Die Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt das Prinzip des Schießverfahrens
am Beispiel der 2. geodätischen Hauptaufgabe. Es sind im weiteren noch geeignete
Näherungswerte für den Startvektor
zeigt das Prinzip des Schießverfahrens
am Beispiel der 2. geodätischen Hauptaufgabe. Es sind im weiteren noch geeignete
Näherungswerte für den Startvektor
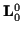 und die Wahl der
Größenordnung der Variationen der Näherungsvektoren sowie deren Änderungen in
der Iterationsphase zu bestimmen. Bei den Größenordnungen der Variationen handelt
es sich um empirisch abzuleitende Werte, auf die im Hinblick auf den Umfang
der Arbeit, hier nicht weiter eingegangen werden soll.
und die Wahl der
Größenordnung der Variationen der Näherungsvektoren sowie deren Änderungen in
der Iterationsphase zu bestimmen. Bei den Größenordnungen der Variationen handelt
es sich um empirisch abzuleitende Werte, auf die im Hinblick auf den Umfang
der Arbeit, hier nicht weiter eingegangen werden soll.
Eine geeignete Näherung für den Tangentenvektor an die geodätische Linie stellt
die Projektion des räumlichen Verbindungsvektors von Anfangspunkt und Endpunkt
in die Tangentialebene der Fläche im Anfangspunkt dar. Hierzu muß zunächst der
Normalenvektor
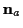 der Fläche im Anfangspunkt A bestimmt werden.
Mit der Normierung
der Fläche im Anfangspunkt A bestimmt werden.
Mit der Normierung
ergibt dich dieser zu
Der orthogonale Abstand des Endpunkts von der Tangentialebene im Anfangspunkt
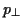 bestimmt sich aus dem Skalarprodukt
bestimmt sich aus dem Skalarprodukt
und der Tangentenvektor selbst über
Die Komponenten dieses Vektors bilden die Näherungswerte für den ersten Schritt
des Schießverfahrens.
Abbildung:
Skizze zur Bestimmung des Tangentenvektors an direkte
Verbindung von A und E
|
|
2.4.2.2 Berechnung der Näherungswerte für
die Länge der geodätischen Linie zwischen Anfangs- und Endpunkt
Die einfachste Möglichkeit besteht in der Annäherung der geodätischen Linie
über einen Kreisabschnitt. Dazu werden aus den kartesischen Koordinaten nach
bekannten Verfahren die ellipsoidischen Koordinaten
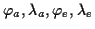 bestimmt und über den Kosinussatz der sphärischen Geometrie, unter Betrachtung
der ellipsoidischen Koordinaten als Kugelkoordinaten, sowie der Annahme
bestimmt und über den Kosinussatz der sphärischen Geometrie, unter Betrachtung
der ellipsoidischen Koordinaten als Kugelkoordinaten, sowie der Annahme
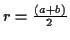 ,
ein Näherungswert für die Länge der geodätischen Linie ermittelt. Es zeigt sich,
daß diese Näherung jedoch, aufgrund der lokalen Konvergenz des Schießverfahrens,
nur ausreichend ist für Strecken bis 5000km, so daß im weiteren die Länge eines
Vertikalschnittes als Näherung Verwendung findet. Die Vertikalschnittebene wird
von
,
ein Näherungswert für die Länge der geodätischen Linie ermittelt. Es zeigt sich,
daß diese Näherung jedoch, aufgrund der lokalen Konvergenz des Schießverfahrens,
nur ausreichend ist für Strecken bis 5000km, so daß im weiteren die Länge eines
Vertikalschnittes als Näherung Verwendung findet. Die Vertikalschnittebene wird
von
 und
und
 in A aufgespannt. Um die
Berechnung zu vereinfachen reicht es aus, das Problem in einem 2-D Koordinatensystem,
in dem sich der Vertikalschnitt als ebene Kurve eindeutig darstellen läßt, zu
betrachten. Ohne näher auf die Transformation einzugehen, sei erwähnt, daß der
Ursprung des Koordinatensystems in den Anfangspunkt A verschoben wurde, die
neue x-Achse in Richtung
in A aufgespannt. Um die
Berechnung zu vereinfachen reicht es aus, das Problem in einem 2-D Koordinatensystem,
in dem sich der Vertikalschnitt als ebene Kurve eindeutig darstellen läßt, zu
betrachten. Ohne näher auf die Transformation einzugehen, sei erwähnt, daß der
Ursprung des Koordinatensystems in den Anfangspunkt A verschoben wurde, die
neue x-Achse in Richtung
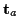 und die neue z-Achse in Richtung
und die neue z-Achse in Richtung
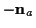 weist. (vgl. hierzu Abb.
weist. (vgl. hierzu Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) Es
ergibt sich die folgende Gleichung für die Vertikalschnittkurve aus der Gleichung
des Ellipsoides im gedrehten ebenen System:
) Es
ergibt sich die folgende Gleichung für die Vertikalschnittkurve aus der Gleichung
des Ellipsoides im gedrehten ebenen System:
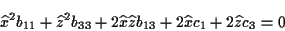
Die Auflösung der quadratischen Gleichung führt zu
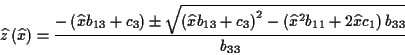 |
(2.11) |
und
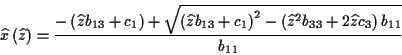 |
(2.12) |
Abbildung:
Intervallteilung zur Berechnung des Vertikalschnitts
|
|
Zur Berechnung der Länge des Verikalschnitts erfolgt eine Einteilung der z-Achse
des ebenen Systems gem. Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) in
in 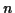 Teilintervalle
Teilintervalle
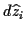 . Über (
. Über (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) werden die zugehörigen
Koordinatendifferentiale
) werden die zugehörigen
Koordinatendifferentiale 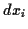 ermittelt und mit den erhaltenen Werten
dann die Streckendifferentiale
ermittelt und mit den erhaltenen Werten
dann die Streckendifferentiale
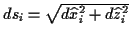 . Die gesuchte Strecke ergibt sich demzufolge nach
. Die gesuchte Strecke ergibt sich demzufolge nach
Die Abbildung ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt, daß es numerisch sinnvoll ist,
das gesamte Integrationsintervall in 3 Teilintervalle zu ordnen. Im ersten,
sowie im dritten wird
zeigt, daß es numerisch sinnvoll ist,
das gesamte Integrationsintervall in 3 Teilintervalle zu ordnen. Im ersten,
sowie im dritten wird 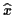 , im zweiten
, im zweiten  als
unabhängige Variable gewählt. Damit findet bei der Berechnung der Koordinatendifferentiale
im zweiten Intervall Gleichung (
als
unabhängige Variable gewählt. Damit findet bei der Berechnung der Koordinatendifferentiale
im zweiten Intervall Gleichung (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ), in den übrigen
Gleichung (
), in den übrigen
Gleichung (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) Verwendung. Im ersten Intervall erhält
(
) Verwendung. Im ersten Intervall erhält
(![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) das Vorzeichen ``+'', im dritten ``-``.
Die Genauigkeit der Berechnung ist abhängig von der Zahl
) das Vorzeichen ``+'', im dritten ``-``.
Die Genauigkeit der Berechnung ist abhängig von der Zahl  der Teilintervalle
der Teilintervalle
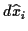 bzw.
bzw.
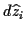 .
.
Mit dem, auf diese Weise ermittelten Näherungswert für die Länge der geodätischen
Linie zwischen Anfangspunkt A und Endpunkt E auf einem durch seine Parameter
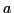 und
und 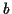 gegebenem Ellipsoid, kann die 2. geodätische Hauptaufgabe
nach dem Schießverfahren gelöst werden2.15.
gegebenem Ellipsoid, kann die 2. geodätische Hauptaufgabe
nach dem Schießverfahren gelöst werden2.15.
Die Vorgehensweise des MATLAB-Programms guirwp_graphik.m zur Berechnung
der 2. geodätischen Hauptaufgabe entspricht weitestgehend den in den Abschnitten
zuvor erwähnten Verfahren. Die Anfangswertaufgaben werden mit RK7multi.m
gelöst und zusätzlich wird zu Beginn, um die Intervallteilung bei der Berechnung
des Vertikalschnitts durchzuführen, die Länge eines Kreisabschnitts ermittelt.
Das zur Bedienung des Programms erstellte GUI (siehe Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
enthält Eingabefelder für
)
enthält Eingabefelder für
- vorzugebende kartesische Koordinaten des Anfangs- und Endpunktes als Randwerte
- Maße des zugrundezulegenden Ellipsoides
- Schranke für den euklidschen Abstand der ermittelten Endpunktkoordinaten von
den vorgegebenen Randwerten als Abbruchkriterium für das Schießverfahren
- die zu wählende Intervallbreite bei der Berechnung der Länge des Vertikalschnittes
- Größe der relativen Variationen von
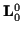 (in der Oberfläche
mit dsigma bezeichnet) in der ersten Iteration des Schießverfahrens
(in der Oberfläche
mit dsigma bezeichnet) in der ersten Iteration des Schießverfahrens
- einen Änderungsfaktor für die relativen Variationen
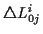
Ausgegeben werden
- die Ergebnisse der Berechnung des Vertikalschnittes
- die Zahl der benötigten Iterationen
- der über die Kreisabschnittsberechnung abgeschätzte Entfernungsbereich
- die Länge, sowie die Azimute der geodätischen Linie zwischen A und E
Zunächst sei erwähnt, daß alle auftretenden Routinen als Funktionen realisiert
sind, d.h., daß die in den Zwischenschritten berechneten Ergebnisse am Ende
des Programmablaufs keiner weiteren Anwendung mehr zur Verfügung stehen2.16. Um die Berechnung zu starten, kann entweder an der Eingabeaufforderung das
Script guirwp_graphik.m aufgerufen werden oder man startet das komplette
Paket durch den Aufruf von geod_haupt.m. Beide Scripte dienen dem
Aufbau der graphischen Benutzeroberflächen. Mit der Berechnung der 2. geodätischen
Hauptaufgabe, wird nach Eingabe der Randwerte und der Steuerparameter in die
Oberfläche, durch Anklicken des Startbuttons mit automatischem Aufruf der Funktion
geo_haupt_2_graphik.m begonnen. Diese Funktion besitzt keine Ausgabewerte
sondern dient nur zur Berechnung der Randwertaufgabe sowie als Schnittstelle
für das GUI. Nach Auslesen der eingegebenen Daten wird zunächst das Fenster
initialisiert und eine erste Abschätzung der Entfernung wird über die Länge
eines Kreisbogens vorgenommen. Diese Abschätzung dient der Näherungswertberechnung
über den Vertikalschnitt zur Bestimmung der Intervallteilung2.17. Die Berechnung erfolgt durch die Funktion kreisbogen.m welche die
Länge eines Kreisbogens zwischen den Vektoren des Anfangs- und des Endpunktes
bezüglich einer Kugel mit dem Radius
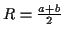 ermittelt.
ermittelt.
Abbildung:
Flußdiagramm zur Berechnung der 2. geodätischen Hauptaufgabe
|
|
Nach dieser groben Ermittlung wird die Funktion vertikalschnitt.m,
die die Länge des Vertikalschnittes und dessen Richtung am Anfangs- sowie am
Endpunkt berechnen soll, aufgerufen. Übergeben werden hier nur die Koordinaten
des Anfangs- und Endpunktes, die übrigen Steuerparameter wurden in der aufrufenden
Funktion zuvor als global deklariert. Wie im Abschnitt auf Seite ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) beschrieben, müssen, vor der Berechnung der Strecken, die Tangentenvektoren
für die Transformation der Ellipse in das ebene System bestimmt werden. Dies
geschieht durch die Funktion kart_lokal.m, die als Eingabewerte wiederum
die Koordinaten der Randpunkte verarbeitet. Da die Tangentenvektoren weiterhin
verwendet werden, besitzt kart_lokal.m ebenfalls keine Ausgabeparamter,
sondern ändert nur die von vornherein als global deklarierten Variablen. Die
Berechnung der Länge des Vertikalschnittes erfolgt nach Ablauf von kart_lokal.m
wieder in vertikalschnitt.m. Je nach Lage des Endpunktes müssen unter
Berücksichtigung der über die Funktion kreisbogen.m erhaltenen Abschätzung
die Streckenanteile in den einzelnen Integrationsintervallen berechnet werden.
Ohne weiter auf die Berechnung, die schon zuvor beschrieben wurde, einzugehen,
sei erwähnt, daß diese von einzelnen kleineren Hilfsfunktionen, deren Quellcode
der beigefügten Diskette entnommen werden kann, durchgeführt wird. Zum Schluß
der Berechnung werden die zur Lösung des Anfangswertproblems nötigen Näherungswerte
beschrieben, müssen, vor der Berechnung der Strecken, die Tangentenvektoren
für die Transformation der Ellipse in das ebene System bestimmt werden. Dies
geschieht durch die Funktion kart_lokal.m, die als Eingabewerte wiederum
die Koordinaten der Randpunkte verarbeitet. Da die Tangentenvektoren weiterhin
verwendet werden, besitzt kart_lokal.m ebenfalls keine Ausgabeparamter,
sondern ändert nur die von vornherein als global deklarierten Variablen. Die
Berechnung der Länge des Vertikalschnittes erfolgt nach Ablauf von kart_lokal.m
wieder in vertikalschnitt.m. Je nach Lage des Endpunktes müssen unter
Berücksichtigung der über die Funktion kreisbogen.m erhaltenen Abschätzung
die Streckenanteile in den einzelnen Integrationsintervallen berechnet werden.
Ohne weiter auf die Berechnung, die schon zuvor beschrieben wurde, einzugehen,
sei erwähnt, daß diese von einzelnen kleineren Hilfsfunktionen, deren Quellcode
der beigefügten Diskette entnommen werden kann, durchgeführt wird. Zum Schluß
der Berechnung werden die zur Lösung des Anfangswertproblems nötigen Näherungswerte
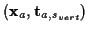 in einem Vektor
an die Ursprungsfunktion geo_haupt_2_graphik.m übergeben. Vor dem
Start der Iteration erfolgt dann dort, mit Initialisierung der Abbruchbedingung
(siehe Seite
in einem Vektor
an die Ursprungsfunktion geo_haupt_2_graphik.m übergeben. Vor dem
Start der Iteration erfolgt dann dort, mit Initialisierung der Abbruchbedingung
(siehe Seite ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ), die erste Berechnung des AWP's
mit den o.g. Näherungswerten. Die Berechnung der Randbedingungen (
), die erste Berechnung des AWP's
mit den o.g. Näherungswerten. Die Berechnung der Randbedingungen (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ),
bzw. der Soll-Ist Abgleich, wird von der gleichnamigen Funktion randbedingungen.m
durchgeführt. Danach startet das Schießverfahren mit den einzelnen Berechnungen
der Anfangswertaufgaben, wobei in jedem Schritt auf 2 verschiedene Arten eine
Überprüfung auf Divergenz, sowie eine Abfrage nach Zutreffen des Abbruchkriteriums
erfolgt. Wird dieses erfüllt endet die Iteration, die Ergebnisse werden an die
Benutzerschnittstelle übergeben und es erscheint die Meldung Berechnung
beeendet.
),
bzw. der Soll-Ist Abgleich, wird von der gleichnamigen Funktion randbedingungen.m
durchgeführt. Danach startet das Schießverfahren mit den einzelnen Berechnungen
der Anfangswertaufgaben, wobei in jedem Schritt auf 2 verschiedene Arten eine
Überprüfung auf Divergenz, sowie eine Abfrage nach Zutreffen des Abbruchkriteriums
erfolgt. Wird dieses erfüllt endet die Iteration, die Ergebnisse werden an die
Benutzerschnittstelle übergeben und es erscheint die Meldung Berechnung
beeendet.
Abbildung:
Graphische Benutzeroberfläche zur Lösung der 2. geodätischen
Hauptaufgabe
|
|
In Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) werden die Ergebnisse, wie auch schon
bei der ersten Hauptaufgabe, Aringers Daten gegenübergestellt. Die der Berechnung
zugrundeliegenden Ellipsoidparameter waren
werden die Ergebnisse, wie auch schon
bei der ersten Hauptaufgabe, Aringers Daten gegenübergestellt. Die der Berechnung
zugrundeliegenden Ellipsoidparameter waren
und
Die Randwerte für die Berechnung über guirwp_graphik.m, bildeten
die von Aringer mit 3 Nachkommastellen angegebenen Koordinaten. Die vorzugebende
Genauigkeit zur Lösung der Anfangswertaufgaben während des Schießverfahrens
wurde mit 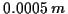 angesetzt. Das Programm beendete die Iteration,
wenn der berechnete Endpunkt um weniger als
angesetzt. Das Programm beendete die Iteration,
wenn der berechnete Endpunkt um weniger als 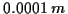 vom Sollwert entfernt
war. Die für die Vertikalschnittberechnung nötige Intervallbreite betrug
vom Sollwert entfernt
war. Die für die Vertikalschnittberechnung nötige Intervallbreite betrug 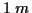 .
Für die relative Größe der Variationen der Komponenten des Tangenteneinheitsvektors,
hat sich ein Wert von
.
Für die relative Größe der Variationen der Komponenten des Tangenteneinheitsvektors,
hat sich ein Wert von
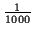 , für Variation der der Strecke von
, für Variation der der Strecke von
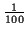 als zweckmäßig erwiesen2.18. Der Veränderungsfaktor wurde mit
als zweckmäßig erwiesen2.18. Der Veränderungsfaktor wurde mit 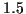 angesetzt. An dieser Stelle sei
darauf hingewiesen, daß alle Veränderungen der mit den Variationen der Anfangswerte
zusammenhängenden Steuerparameter, einen sehr großen Einfluß auf das Konvergenzverhalten
des Schießverfahrens haben. Um hier jedoch einen funktionalen Zusammenhang abzuleiten,
bedarf es weiterer Untersuchungen die den Umfang dieser Arbeit überschreiten.
angesetzt. An dieser Stelle sei
darauf hingewiesen, daß alle Veränderungen der mit den Variationen der Anfangswerte
zusammenhängenden Steuerparameter, einen sehr großen Einfluß auf das Konvergenzverhalten
des Schießverfahrens haben. Um hier jedoch einen funktionalen Zusammenhang abzuleiten,
bedarf es weiterer Untersuchungen die den Umfang dieser Arbeit überschreiten.
Wie der Tabelle zu entnehmen ist, differieren die Ergebnisse für die Azimute
im Bereich von 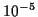 Sekunden. Die Entfernung wird im Gegensatz dazu
identisch erhalten. Es verwundert, daß Aringer bei den Beispielen 2 - 6 das
Azimut auf die 7-te Nachkommastelle genau betimmen kann (vgl. Beispiele für
die 1. geodätische Hauptaufgabe), obwohl er die Koordinaten des Endpunktes,
die er aus der Berechnung der Anfangswertaufgaben ermittelt hat, nur mit 3 Nachkommastellen
ansetzt. Das führt dazu, daß der Vergleich der Ergebnisse nicht besonders aussagekräftig
ist.
Sekunden. Die Entfernung wird im Gegensatz dazu
identisch erhalten. Es verwundert, daß Aringer bei den Beispielen 2 - 6 das
Azimut auf die 7-te Nachkommastelle genau betimmen kann (vgl. Beispiele für
die 1. geodätische Hauptaufgabe), obwohl er die Koordinaten des Endpunktes,
die er aus der Berechnung der Anfangswertaufgaben ermittelt hat, nur mit 3 Nachkommastellen
ansetzt. Das führt dazu, daß der Vergleich der Ergebnisse nicht besonders aussagekräftig
ist.
Um die Integrität des Programmsystems zu prüfen, wurden einige Anfangswertaufgaben
berechnet und die Ergebnisse ungerundet in das Programm zur Lösung
der Randwertaufgabe übernommen. Dabei konnte keine Differenz, außerhalb des
Rahmens der Rechengenauigkeit, festgestellt werden.
Abbildung:
Aufbau des Programmsystems
|
|
Abbildung:
Benutzeroberfläche des Programmsystems
|
|
Der Aufgabenstellung entsprechend wurde unter MATLAB ein Programmsystem2.19 erstellt, das einem Nutzer erlaubt, geometrische, wie auch numerische Eigenschaften
von geodätischen Linien auf einem Rotationsellipsoid zu untersuchen. Um auch
im Umgang mit MATLAB unerfahrenen Benutzern die Anwendung zu ermöglichen, wurde
das System mit einer graphischen Benutzeroberfläche (GUI) versehen. Diese erlaubt
einen interaktiven Zugriff auf MATLABs interne Grafikfunktionen, ohne daß ein
Benutzer sich vorher intensiv mit der Programmiersystem auseinandersetzen muß.
Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt das Hauptfenster des Systems, wie es sich, nach
Eingabe von geod_haupt am MATLAB-Prompt, öffnet. Mit Hilfe dieser
Oberfläche lassen sich nun folgende Aufgaben lösen:
zeigt das Hauptfenster des Systems, wie es sich, nach
Eingabe von geod_haupt am MATLAB-Prompt, öffnet. Mit Hilfe dieser
Oberfläche lassen sich nun folgende Aufgaben lösen:
- Berechnung der 1. geodätischen Hauptaufgabe
- Berechnung der 2. geodätischen Hauptaufgabe
- Berechnung von Punkten auf einer geodätischen Linie und deren Abspeicherung
in einer Datei
- Eine dreidimensionale Darstellung des Verlaufs von geodätischen Linien2.20 auf dem zugrundeliegenden Ellipsoid
- Eine dreidimensionale Visualisierung eines Parallelkoordinatensystems in Soldnerscher
Anordnung
Da die Berechnung der Hauptaufgaben schon in den vorangegangenen Abschnitten
erläutert wurde, sei im folgenden kurz auf die Punkte 3-5 eingegangen.
Das Programm zur Darstellung der Ephemeriden wird jeweils nach der Berechnung
der ersten bzw. zweiten geodätischen Hauptaufgabe aus den Oberflächen heraus
gestartet. Nach der Wahl des Tastenfeldes Ephemeridenberechnung öffnet
sich das Fenster in Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) . Hier wird zum einen die gewünschte
Zahl der Stützpunkte2.21 der geodätischen Linie eingetragen, zum anderen besteht die Möglichkeit zwischen
zwei Arten der Darstellung des Ellipsoides zu wählen. In der Gitterdarstellung
werden nur die, über eine Hilfsfunktion berechneten Stützpunkte eines geographischen
ellipsoidischen Koordinatensystems mit Linien verbunden, dargestellt. Über die
Zahl der Stützstellen läßt sich frei verfügen. Bei der Flächendarstellung hingegen
werden diese Gitterelemente farbig ausgefüllt, was dazu führt, daß die später
zwischen die Stützpunkte gezeichneten Verbindungslinien nicht mehr komplett
sichtbar sind.
. Hier wird zum einen die gewünschte
Zahl der Stützpunkte2.21 der geodätischen Linie eingetragen, zum anderen besteht die Möglichkeit zwischen
zwei Arten der Darstellung des Ellipsoides zu wählen. In der Gitterdarstellung
werden nur die, über eine Hilfsfunktion berechneten Stützpunkte eines geographischen
ellipsoidischen Koordinatensystems mit Linien verbunden, dargestellt. Über die
Zahl der Stützstellen läßt sich frei verfügen. Bei der Flächendarstellung hingegen
werden diese Gitterelemente farbig ausgefüllt, was dazu führt, daß die später
zwischen die Stützpunkte gezeichneten Verbindungslinien nicht mehr komplett
sichtbar sind.
Abbildung:
Auswahlfenster zur Ephemeridenberechnung
|
|
Die Genauigkeit, mit der die Zwischenpunkte berechnet werden, richtet sich nach
der Genauigkeit, die für die Berechnung der Hauptaufgaben angesetzt wurde. Zur
Verkürzung der Rechenzeit wird die empirische Iterationsfunktion für jeden Stützpunkt
einzeln ausgewertet. Die Endpunktkoordinaten werden außerdem zur Kontrolle ein
zweites Mal ermittelt. Nach der Bestätigung der Eingabe in Fenster Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) startet das Script ephemeridenberechnung.m, es öffnet sich das Fenster
mit der dreidimensionalen Darstellung des Ellipsoides, sowie das Fenster in
Abb.
startet das Script ephemeridenberechnung.m, es öffnet sich das Fenster
mit der dreidimensionalen Darstellung des Ellipsoides, sowie das Fenster in
Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) . Diesem kann während der Berechnung die Nummer
des aktuell ermittelten Punktes entnommen werden. Parallel dazu werden im Grafikfenster
die Stützpunkte als rote Kreuze geplottet.
. Diesem kann während der Berechnung die Nummer
des aktuell ermittelten Punktes entnommen werden. Parallel dazu werden im Grafikfenster
die Stützpunkte als rote Kreuze geplottet.
Abbildung:
GUI zum Steuern der Ephemeridendarstellung und
Abspeichern der Stützpunktkoordinaten
|
|
Die Richtung des Blickpunktes wird automatisch in Richtung des Anfangspunktvektors
gesetzt, so daß die Linie vollständig im Blickfeld des Betrachters erscheint.
Anfangs- sowie Endpunkt werden durch einen, grün dargestellten, räumlichen Vektor
hervorgehoben.
Am Ende der Berechnungen können die kartesischen Koordinaten der Zwischenpunkte
in einer binären MATLAB-Workspace (*.mat) Datei abgespeichert werden2.22. Hierbei ist zu beachten, daß falls mehrere Linien in einer Datei zusammengefaßt
werden, diese sich auf dasselbe Ellipsoid beziehen sollten, da die Ellipsoidparameter
ebenfalls dort abgelegt werden. Der Dateiname muß mit voller Pfadangabe, aber
ohne Erweiterung angegeben werden.
Über die Grafikoptionen im unteren Bereich des Steuerungsfensters läßt sich
der Blickpunkt sowie ein gewünschter Zoomfaktor für die Darstellung festlegen.
Abbildung ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt das graphische Ergebnis einer Ephemeridenberechnung
mit 20 Stützstellen bei einer Länge der geodätischen Linie von 15000km.
zeigt das graphische Ergebnis einer Ephemeridenberechnung
mit 20 Stützstellen bei einer Länge der geodätischen Linie von 15000km.
Abbildung:
Darstellung einer Ephemeride
|
|
Im Hauptfenster gelangt man durch Wahl des Schalters geod_plot zu
einer Möglichkeit mehrere, im Anschluß an die Berechnung der Hauptaufgaben abgespeicherte
Linienverläufe,
Abbildung:
Darstellungsschnittstelle
|
|
darzustellen. (Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt die zugehörige Oberfläche) Durch
Angabe des gewünschten Dateinamens im Rahmen Datensatz und
anschließender Wahl des Schalters Laden wird der Inhalt der Datei im
darunter liegenden Auswahlfenster angezeigt. Sollen mehrere Linien innerhalb
einer Grafik dargestellt werden, so muß unter den Plotoptionen
das Feld hinzufügen angewählt sein. Das im Anschluß daran vorliegende
dreidimensionale Modell kann mit Hilfe der Maus beliebig um seine 3 Achsen gedreht
werden. Die Art der Darstellung der Ephemeride ist frei wählbar.
zeigt die zugehörige Oberfläche) Durch
Angabe des gewünschten Dateinamens im Rahmen Datensatz und
anschließender Wahl des Schalters Laden wird der Inhalt der Datei im
darunter liegenden Auswahlfenster angezeigt. Sollen mehrere Linien innerhalb
einer Grafik dargestellt werden, so muß unter den Plotoptionen
das Feld hinzufügen angewählt sein. Das im Anschluß daran vorliegende
dreidimensionale Modell kann mit Hilfe der Maus beliebig um seine 3 Achsen gedreht
werden. Die Art der Darstellung der Ephemeride ist frei wählbar.
Tabelle:
Zuordnung der Linientypen
| Symbol |
Linientyp |
| - |
durchgezogen |
| - |
gestrichelt |
| : |
gepunktet |
| -. |
abwechselnd |
| none |
keine Darstellung |
|
Tabelle:
Zuordnung der Punktsymbole
| Symbol |
Punktbeschreibung |
| + |
Plus |
| o |
Kreis |
| * |
Stern |
| x |
Kreuz |
| s |
Quadrat |
| d |
Raute |
| h |
Hexagramm |
| . |
Punkt |
|
Tabelle:
Zuordnung der Farben
| Abbkürzung |
Farbe |
| k |
Schwarz |
| w |
Weiß |
| r |
Rot |
| g |
Grün |
| b |
Blau |
| y |
Gelb |
| c |
Cyan |
| m |
Magenta |
|
Da es programmiertechnisch einfacher war in den Auswahlfenstern die MATLAB spezifischen
Abbkürzungen für Farbe und Form der graphischen Objekte anzeigen zu lassen,
sind die entsprechenden Zuordnungen in den Tabellen ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) -
-![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) kurz aufgeführt.
kurz aufgeführt.
Abbildung:
Darstellung mehrerer Ephemeriden nach Auslesen der Datensätze
|
|
Ein Beispiel für die Darstellung mehrerer Ephemeriden zeigt Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) .
.
Die zum Programmsystem gehörende Funktion Soldner.m dient der Untersuchung
des Verlaufs von geodätischen Linien in der Nähe des Querpols eines globalen
Parallelkoordinatensystems in Soldnerscher Anordnung.
Bei einem allgemeinen geodätischen Parallelkoordinatensystem auf einem Rotationsellipsoid
findet als Abzissenlinie, der durch den Koordinatenanfangspunkt verlaufende
Meridian Verwendung. Die Lage eines Punktes wird durch die Bogenlänge auf der
Abzissenlinie, sowie die Länge einer geodätischen Linie durch diesen Punkt,
die die Abzissenlinie senkrecht schneidet, bestimmt.
Abbildung:
Prinzip eines Parallelkoordinatensystems in Soldnerscher
Anordnung
|
|
Dabei entspricht 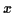 der Bogenlänge auf der Abzissenlinie, gemessen vom
Koordinatenanfangspunkt
der Bogenlänge auf der Abzissenlinie, gemessen vom
Koordinatenanfangspunkt 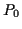 zum Fußpunkt
zum Fußpunkt 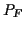 und
und 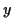 der Länge der geodätischen Linie durch
der Länge der geodätischen Linie durch 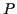 und
und 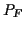 . (vgl. Abb.
. (vgl. Abb.
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
)
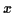 und
und 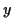 werden in diesem Zusammenhang als die ellipsoidischen
Parallelkoordinaten des Punktes
werden in diesem Zusammenhang als die ellipsoidischen
Parallelkoordinaten des Punktes 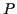 bezeichnet. Sie lassen sich als Gaußsche
Flächenparameter auf dem Ellipsoid interpretieren. Die als Ordinatenlinien bezeichneten
geodätischen Linien verlaufen auf dem Ellipsoid weder eben noch sind es geschlossene
Kurven. Ebenso bilden die Abzissenlinien oder geodätische Parallelen, zwar geschlossene,
jedoch keine ebenen Kurven. An Stelle des Querpols, der sich bei Einführung
eines Parallelkoordinatensystems als Schnittpunkt der Geodäten auf der Kugel
ergibt, bildet sich im Falle eines Rotationsellipsoides ein, zum Äquator symmetrisches
Gebiet, das durch eine asteroidenförmige Flächenkurve begrenzt wird. Mit Hilfe
des im folgenden beschriebenen Programms läßt sich diese Figur anhand eines
dreidimensionalen Gittermodells des Koordinatennetzes in Abhängigkeit gewisser
Parameter graphisch darstellen.
bezeichnet. Sie lassen sich als Gaußsche
Flächenparameter auf dem Ellipsoid interpretieren. Die als Ordinatenlinien bezeichneten
geodätischen Linien verlaufen auf dem Ellipsoid weder eben noch sind es geschlossene
Kurven. Ebenso bilden die Abzissenlinien oder geodätische Parallelen, zwar geschlossene,
jedoch keine ebenen Kurven. An Stelle des Querpols, der sich bei Einführung
eines Parallelkoordinatensystems als Schnittpunkt der Geodäten auf der Kugel
ergibt, bildet sich im Falle eines Rotationsellipsoides ein, zum Äquator symmetrisches
Gebiet, das durch eine asteroidenförmige Flächenkurve begrenzt wird. Mit Hilfe
des im folgenden beschriebenen Programms läßt sich diese Figur anhand eines
dreidimensionalen Gittermodells des Koordinatennetzes in Abhängigkeit gewisser
Parameter graphisch darstellen.
Abbildung:
GUI zur Darstellung eines Soldner'schen Koordinatensystems
|
|
Das Programm kann entweder von der Eingabeaufforderung durch Aufruf des Skriptes
soldner_graphik.m oder im Hauptfenster des Programmsystems, durch
Wahl des Schalters soldner, gestartet werden. Über das Steuerfenster
(siehe Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) lassen sich die Ellipsoidparameter, die
Zahl der Stützpunkte des Koordinatensystems, sowie die Genauigkeit der Berechnung
festlegen. Die Berechnung wird durch Auswahl des Buttons Plotten, der
das Script Soldner.m aufruft, begonnen. Zunächst wird der Bezugsmeridian
) lassen sich die Ellipsoidparameter, die
Zahl der Stützpunkte des Koordinatensystems, sowie die Genauigkeit der Berechnung
festlegen. Die Berechnung wird durch Auswahl des Buttons Plotten, der
das Script Soldner.m aufruft, begonnen. Zunächst wird der Bezugsmeridian
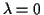 entsprechend der Wahl der Breitenteilung in Intervalle aufgeteilt.
Dabei sei anzumerken, daß durch eine solche Teilung zwar keine gleichen Längenteilung
des Bezugmeridians erreicht wird, jedoch ist dies für die Darstellung der Figur
auch nicht erforderlich. Da es sich bei dem zugrundegelegten Ellipsoid um einen
rotationssymetrischen Körper handelt, reicht es aus, die Stützpunkte des Koordinatennetzes
für nur einen Oktanten dieses Körpers zu berechnen und die anderen durch Spiegelungen
abzuleiten. Im Programm selbst werden für die einzelnen Stützpunkte des Bezugsmeridians
sukzessive Anfangswertaufgaben für ein Azimut von
entsprechend der Wahl der Breitenteilung in Intervalle aufgeteilt.
Dabei sei anzumerken, daß durch eine solche Teilung zwar keine gleichen Längenteilung
des Bezugmeridians erreicht wird, jedoch ist dies für die Darstellung der Figur
auch nicht erforderlich. Da es sich bei dem zugrundegelegten Ellipsoid um einen
rotationssymetrischen Körper handelt, reicht es aus, die Stützpunkte des Koordinatennetzes
für nur einen Oktanten dieses Körpers zu berechnen und die anderen durch Spiegelungen
abzuleiten. Im Programm selbst werden für die einzelnen Stützpunkte des Bezugsmeridians
sukzessive Anfangswertaufgaben für ein Azimut von 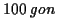 und einer
Streckenteilung gemäß der Auswahl im Fenster für ein Intervall von
und einer
Streckenteilung gemäß der Auswahl im Fenster für ein Intervall von 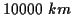 gelöst. Dabei ist zu beachten daß, falls ein Rotationsellipsoid einer anderen
Größenordnung als der eines Erdellipsoides gewählt wird, dieser Wert im Quellcode
sinnvoll abzuändern ist. Die Auswahl der Genauigkeit dient in diesem Fall einer
Steigerung der Rechengeschwindigkeit. Auch hier wird die Iterationsfunktion
für jedes einzelne AWP erneut ausgewertet und die auf diese Weise ermittelte
Zahl der notwendigen Iterationen wird der Berechnung zugrundegelegt. Tabelle
gelöst. Dabei ist zu beachten daß, falls ein Rotationsellipsoid einer anderen
Größenordnung als der eines Erdellipsoides gewählt wird, dieser Wert im Quellcode
sinnvoll abzuändern ist. Die Auswahl der Genauigkeit dient in diesem Fall einer
Steigerung der Rechengeschwindigkeit. Auch hier wird die Iterationsfunktion
für jedes einzelne AWP erneut ausgewertet und die auf diese Weise ermittelte
Zahl der notwendigen Iterationen wird der Berechnung zugrundegelegt. Tabelle
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) zeigt jeweils 4 verschiedene Ansichten eines Modells,
wie es sich nach Ablauf der Berechnung dem Betrachter darstellt.
zeigt jeweils 4 verschiedene Ansichten eines Modells,
wie es sich nach Ablauf der Berechnung dem Betrachter darstellt.
Tabelle:
Koordinatennetz eines Parallelkoordinatensystems
in Soldnerscher Anordnung
|
|
Nach dem Satz von Clairaut läßt sich der Verlauf einer geodätischen
Linie auf einem rotationsymmetrischen Körper beschreiben mit
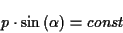 |
(2.13) |
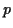 entspricht dabei dem Parallelkreishalbmesser, der sich ausgedrückt,
durch die reduzierte Breite
entspricht dabei dem Parallelkreishalbmesser, der sich ausgedrückt,
durch die reduzierte Breite 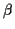 , darstellen läßt über
, darstellen läßt über
Gilt 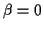 , und bezeichne
, und bezeichne
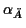 das Azimut der
geodätischen Linie am Äquator, so folgt
das Azimut der
geodätischen Linie am Äquator, so folgt 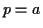 und für (
und für (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
folgt
)
folgt
Die Konstante 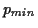 entspricht dabei dem minimalen Parallelkreishalbmesser,
der von der geodätischen Linie nicht unterschritten wird. Diesem entspricht
die maximale reduzierte Breite
entspricht dabei dem minimalen Parallelkreishalbmesser,
der von der geodätischen Linie nicht unterschritten wird. Diesem entspricht
die maximale reduzierte Breite
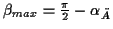 ,die
nicht überschritten wird. Damit schwingt die geodätische Linie, mit
einer von der Abplattung
,die
nicht überschritten wird. Damit schwingt die geodätische Linie, mit
einer von der Abplattung 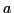 und dem Azimut
und dem Azimut
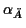 abhängigen
Periode, symmetrisch zum Äquator zwischen den reduzierten Breiten
abhängigen
Periode, symmetrisch zum Äquator zwischen den reduzierten Breiten 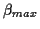 und
und 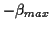 .
.
Mit Hilfe des Darstellungsprogramms für den Verlauf geodätischer Linien läßt
sich dieses Verhalten graphisch veranschaulichen. Es wurden für ein Ellipsoid
mit den Parametern
4 Lösungen der ersten geodätischen Hauptaufgabe für die Azimute
 und
und 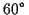 bestimmt. Das Integrationsintervall betrug dabei
bestimmt. Das Integrationsintervall betrug dabei  . Der Ortsvektor des Startpunktes lautet
. Der Ortsvektor des Startpunktes lautet
Abbildung ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) bietet eine dreidimensionale Aufsicht der
sich ergebenden Darstellung. Zur besseren Unterscheidung der Linien seien zusätzlich
die 2 Projektionen in Form der Abbildungen
bietet eine dreidimensionale Aufsicht der
sich ergebenden Darstellung. Zur besseren Unterscheidung der Linien seien zusätzlich
die 2 Projektionen in Form der Abbildungen ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) und
und ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) beigefügt. Die farbliche Zuordnung der Linien, sowie die zugehörigen Werte für
die maximalen Breiten sind Tabelle
beigefügt. Die farbliche Zuordnung der Linien, sowie die zugehörigen Werte für
die maximalen Breiten sind Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) 2.23 zu entnehmen.
2.23 zu entnehmen.
Abbildung:
Veranschaulichung der geometrischen Bedeutung des
Satzes von Clairaut für den Verlauf der geodätischen Linien
|
|
Abbildung:
Projektion der Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) in
die
in
die
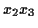 -Ebene
-Ebene
|
|
Abbildung:
Projektion der Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) in die
in die
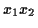 -Ebene
-Ebene
|
|
Der Arbeit sind als Anhang die wichtigsten MATLAB-Scripte, die schon im Flußdiagramm
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) bezeichnet wurden, beigefügt. Zur Programmierung der
Oberfläche kann leider kein Quellcode abgegeben werden, da diese interaktiv,
per Drag & Drop, geschieht und hierbei zusätzlich entstehender Code in binären
Dateien abgespeichert wird. Als Beispiel für ein, bei der Oberflächenprogrammierung
automatisch von MATLAB erstelltes Script, kann der Ausdruck der Datei liniendarstellung.m,
welche den Aufbau der Oberfläche aus Abb.
bezeichnet wurden, beigefügt. Zur Programmierung der
Oberfläche kann leider kein Quellcode abgegeben werden, da diese interaktiv,
per Drag & Drop, geschieht und hierbei zusätzlich entstehender Code in binären
Dateien abgespeichert wird. Als Beispiel für ein, bei der Oberflächenprogrammierung
automatisch von MATLAB erstelltes Script, kann der Ausdruck der Datei liniendarstellung.m,
welche den Aufbau der Oberfläche aus Abb. ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) regelt, ebenfalls
dem Anhang entnommen werden.
regelt, ebenfalls
dem Anhang entnommen werden.
- 1
- Aringer, K. (1994): Geodätische Hauptaufgaben auf Flächen in kartesischen Koordinaten.
DGK C 421.
- 1
- Heck, B. (1993): Rechenverfahren und Auswertemodelle der Landesvermessung. H.
Wichmann Verlag, Karlsruhe.
- 1
- Heil M., Kitzka F. (1984): Grundkurs Theoretische Mechanik. B.G. Teubner, Stuttgart.
- 2
- Heitz, S., Stöcker-Meier, E. (1998): Grundlagen der Physikalischen Geodäsie.
Dümmler, Bonn.
- 3
- Klingbeil, E. (1989): Tensorrechnung für Ingenieure. B.I.-Hochschultaschenbuch
Band 197, Mannheim, Wien, Zürich.
- 4
- Klotz, J. (1991): Eine analytische Lösung kanonischer Gleichungen der geodätischen
Linie zur Transformation geodätischer Flächenkoordinaten. DGK C 385.
- 5
- Moritz, H., Hofmann-Wellenhof, B. (1993): Geometry, Relativity, Geodesy. H.
Wichmann Verlag, Karlsruhe.
- 6
- Reinhardt F., Soeder H. (1984): dtv-Atlas zur Mathematik.Deutscher Taschenbuch
Verlag, München.
- 6
- Schürer, M. (1975): Die geodätischen Linien und die Mechanik. Vermessung, Photogrammetrie,
Kulturtechnik; Fachblatt III/IV-75.
- 2
- Spiegel, M. R. (1990): Allgemeine Mechanik. McGraw-Hill Book Company GmbH, Hamburg.
- 7
- Script zur Vertiefungsvorlesung im Fach Astronomisch/Physikalische Geodäsie,
WS 1997/98.
Theoretische und numerische Untersuchungen zu den geodätischen Hauptaufgaben
This document was generated using the
LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /home/hannah/Diplomarbeit/Text/Diplomarbeit.tex
The translation was initiated by root on 2000-10-19
Fußnoten
- ... Koordinatensystem1.1
- Ansonsten würde die Eindeutigkeit der Zuordnung der Punkte verloren gehen
- ... Rechenregeln1.2
- KLINGBEIL(1989)
- ... 1.3
- Es handelt sich hier um die Christoffelsymbole 2. Art, die Ableitung dieser
'Objekte des räumlichen Zusammenhanges' aus den Metrikkoeffizienten wird in
einem folgenden Abschnitt eingehender behandelt.
- ... Koeffizienten1.4
- Aus MORITZ, H., HOFMANN-WELLENHOF, B. (1993).
- ... Integratoren1.5
- Ein Vergleich der Leistungsfähigkeit verschiedener Integratoren bei der Lösung
der geodätischen Hauptaufgaben auf einem Rotationsellipsoid ist in ARINGER (1994)
dargestellt.
- ... Prinzip1.6
- Das Prinzip (
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) geht von den s.g. virtuellen
Verschiebungen
) geht von den s.g. virtuellen
Verschiebungen
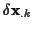 eines Massepunktes
eines Massepunktes 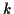 zu
einem festen Zeitpunkt
zu
einem festen Zeitpunkt  aus, und ist daher als differentielles Prinzip
zu betrachten.
aus, und ist daher als differentielles Prinzip
zu betrachten.
- ... bei1.7
- Eine gute Einführung in die unterschiedlichen Methoden der theoretischen Mechanik
bietet HEIL/KITZKA (1984)
- ...
Koordinaten1.8
- Bei diesen kann es sich auch um Winkel, Abstände oder daraus abgeleitete Größen
handeln.
- ... besitzen1.9
- An dieser Stelle ist auf die Analogie zur Definition einer Mannigfaltigkeit
hingewiesen.
- ... klassifiziert1.10
- Beispiel für eine Klassifikation eines mechanischen Systems: Ein Massepunkt
bewege sich reibungslos auf einen langen Draht, welcher mit konstanter Winkelgeschwindigkeit
um eine senkrechte Achse rotiert. In diesem Fall handelt es sich um ein rheonomes,
holonomes und konservatives System.
- ... Zentralgleichung1.11
- Für die Herleitung dieser Gleichung sei auf HEITZ/STÖCKER-MEIER (1998) verwiesen.
- ... Prinzip1.12
- siehe SPIEGEL (1990)
- ... Extremum1.13
- Aufgrund der Tatsache, daß es sich bei diesem meist um ein Minimum handelt,
wird das Prinzip oft als Hamiltonsches Prinzip der kleinsten Wirkung
bezeichnet.
- ... abhängt1.14
- Für diese gilt daher
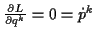
- ... Raum1.15
- Wird auch als pq - Phasenraum bezeichnet.
- ... Parameter1.16
- Diese werden mit den neuen Impulsen
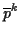 identifiziert.
identifiziert.
- ... Eingesetzt1.17
- Hier sei anzumerken, daß zum besseren Vergleich
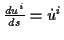 gesetzt wurde
gesetzt wurde
- ... Bestimmungsgleichung1.18
- Diese Gleichung beschreibt den Verlauf einer entfernungsmäßig kürzesten Verbindung,
während in (
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) durch die Transformation
) durch die Transformation
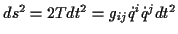 eine kürzeste Verbindung bezüglich des eingeführten Linienelementes beschrieben
wird.
eine kürzeste Verbindung bezüglich des eingeführten Linienelementes beschrieben
wird.
- ... Prismaregel2.1
- Für Runge-Kutta-Verfahren höherer Ordnung findet die Simpsonsche Regel als Verallgemeinerung
der Prismaregel Verwendung.
- ... 2.2
- siehe hierzu ARINGER 1994
- ... Rechenzeit2.3
- siehe hierzu Abb.
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif)
- ...
MIDEVA2.4
- Weitere Informationen zu den Compilern und freie Evaluations-Lizenzen sind erhältlich
unter http://www.mathtools.com.
- ... Schrittweitensteuerung2.5
- Möglichkeiten zur Implementierung einer solchen sind in ARINGER 1994 aufgeführt.
- ...2d_abh_it_von_s_abpl2.6
- Bei der Berechnung wurde hier davon ausgegangen das der Anfangspunkt auf dem
Äquator liegt. Das Azimut wird von Norden nach Osten als positiv angenommen.
Der hier noch nicht variierende Parameter ist die Genauigkeit
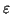 ,
welche für die Berechnung der Graphen mit
,
welche für die Berechnung der Graphen mit 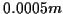 angesetzt wurde.
angesetzt wurde.
- ... verprobt.2.7
- Es sei hier noch einmal bemerkt, daß diese Funktion nur für die diskreten Werte
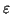 aus Tabelle
aus Tabelle ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) , sowie für
Abplattungen bis
, sowie für
Abplattungen bis  gilt. Ebenso wird der lineare Verlauf der Funktion
gilt. Ebenso wird der lineare Verlauf der Funktion
 auch für Entfernungen über
auch für Entfernungen über 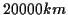 angenommen.
angenommen.
- ... Fehlerschätzung2.8
- Die Schätzung erfolgt über 2 Näherungen der Lösung, welche jeweils über Diskretisierungsverfahren
der globalen Fehlerordnungen
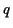 und
und 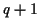 gewonnen werden. Praktisch
wird beim RKF7 ein von Fehlberg angegebener Fehlerterm
gewonnen werden. Praktisch
wird beim RKF7 ein von Fehlberg angegebener Fehlerterm
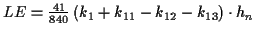 angesetzt, wobei
angesetzt, wobei 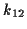 und
und 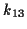 aus zwei weiteren Auswertungen
der Differentialgleichung stammen. Damit ergibt sich der Fehlerterm aus dem
Vergleich eines Verfahrens 8. mit dem eines 7. Ordnung. Über diesen wird bei
ARINGER (1994) die automatische Schrittweitensteuerung implementiert.
aus zwei weiteren Auswertungen
der Differentialgleichung stammen. Damit ergibt sich der Fehlerterm aus dem
Vergleich eines Verfahrens 8. mit dem eines 7. Ordnung. Über diesen wird bei
ARINGER (1994) die automatische Schrittweitensteuerung implementiert.
- ... kann2.9
- Dies führt zu einer geringfügigen Verkürzung der Rechenzeit im Vergleich zu
den Programmen mit Fehlerschätzung.
- ...RKF72.10
- Aus ARINGER (1994), Tabelle 8, wobei hier zu bemerken sei, daß für
diese Berechnung die Vorgabe der Genauigkeit der kartesischen Koordinaten mit
![\( \varepsilon =0.001\left[ m\right] \)](img563.gif) angegeben wurde.
angegeben wurde.
- ... vorkommen2.11
- Bei Vorgabe derselben geforderten Genauigkeit.
- ... Dissertation2.12
- siehe Gleichung (6.61)
- ... werden.2.13
- Um Unklarheiten die im Vergleich mit Aringers Arbeit auftreten können zu vermeiden,
sei erwähnt, daß hier nur das normale Differentialgleichungssystem zur Lösung
der Anfangswertaufgabe Verwendung findet. Der Schritt den Aringer beschreibt
um, wie er es nennt, eine Randwertaufgabe mit freiem Rand auf eine gewöhnliche
Randwertaufgabe zurückzuführen, scheint mir unnötig, außerdem bringt das auf
diese Weise abgeleitete Differentialgleichungsystem, welches mit dem des AWP's
bis auf eine Erweiterung mit der Entfernung
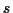 identisch ist, keine brauchbaren
Ergebnisse.
identisch ist, keine brauchbaren
Ergebnisse.
- ... Newtonverfahrens2.14
- Die Grundlage dieses Verfahrens folgt aus einer nach dem linearen Glied abgebrochenen
Taylorentwicklung nach
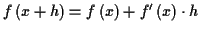 .
Unter der Vorraussetzung, daß
.
Unter der Vorraussetzung, daß
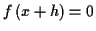 ergibt sich die gesuchte
Größe
ergibt sich die gesuchte
Größe 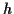 aus
aus
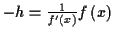 .
Die Gleichung
.
Die Gleichung ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ist dann die Verallgemeinerung für
Funktionen von n-Veränderlichen.
ist dann die Verallgemeinerung für
Funktionen von n-Veränderlichen.
- ... werden2.15
- ARINGER beschreibt in seiner Dissertation die Berechnung des Vertikalschnittbogens
über eine Differentiation von (
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) und (
) und (![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) )
mit anschließender Integration (vgl. Gleichungen (6.55) und (6.56) seiner Arbeit).
Der Sinn dieser Handlungsweise ist mir nicht klar, da ein konstanter Anteil
dadurch wegfällt. Führt man die Integration nach (6.56) formal durch, so ergeben
sich nicht die Ergebnisse die er in seinen Tabellen angibt, sondern man erhält
eine zu kurze Strecke.
)
mit anschließender Integration (vgl. Gleichungen (6.55) und (6.56) seiner Arbeit).
Der Sinn dieser Handlungsweise ist mir nicht klar, da ein konstanter Anteil
dadurch wegfällt. Führt man die Integration nach (6.56) formal durch, so ergeben
sich nicht die Ergebnisse die er in seinen Tabellen angibt, sondern man erhält
eine zu kurze Strecke.
- ... stehen2.16
- Ausgenommen sind hier die über das GUI im Fenster sichtbar oder versteckt übergebenen
Variablenwerte.
- ... Intervallteilung2.17
- Wenn das Programm für andere Ellipsoiddimensionen (6000km < a > 7000km) verwandt
werden soll, so muß hier der Quelltext abgeändert werden, da die Intervallteilung
durch Konstanten festgelegt wurde.
- ... erwiesen2.18
- Um in Beispiel 6 auf nur 12 Schritte zu gelangen, ist für die relative
Variation der Strecke
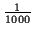 anzusetzen.
anzusetzen.
- ... Programmsystem2.19
- Ein Flußdiagramm das den Aufbau des Programmsystems erläutert, ist in Abb.
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) dargestellt.
dargestellt.
- ... Linien2.20
- Im folgenden wird der Verlauf der Linie in Analogie zur Satellitenbahn als Ephemeride
bezeichnet.
- ... Stützpunkte2.21
- Die Koordinaten dieser Punkte werden über eine Anfangswertaufgabe ermittelt.
- ... werden2.22
- Der Vorteil der binären Dateien liegt darin, daß man in einer solchen, auf einfache
Weise, verschiedene Linien unter eigenen Bezeichnern abspeichern kann. MATLAB
bietet zusätzlich die Möglichkeit diese Datei im ASCII Format auszugeben.
- ...linienzuordnung_clairaut2.23
- Die Berechnung der geographischen Breiten
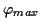 aus den reduzierten
aus den reduzierten
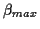 erfolgt nach
erfolgt nach
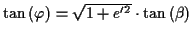 .
.



root
2000-10-19
![]() von
von ![]() Punkten in einem n-dimensionalen
Raum
Punkten in einem n-dimensionalen
Raum ![]() , welche im folgenden mit Mannigfaltigkeit bezeichnet
wird und einen Vektorraum
, welche im folgenden mit Mannigfaltigkeit bezeichnet
wird und einen Vektorraum ![]() , so wird durch die Abbildung von
, so wird durch die Abbildung von ![]() in
in ![]() jeder Punkt einem Vektor zugeordnet. Die Zuordnung setzt eine
Ordnung des Raumes durch eine Vereinbarung über ein System voraus, das als Koordinatensystem
jeder Punkt einem Vektor zugeordnet. Die Zuordnung setzt eine
Ordnung des Raumes durch eine Vereinbarung über ein System voraus, das als Koordinatensystem
![]() bezeichnet wird. Ein Koordinatensystem
bezeichnet wird. Ein Koordinatensystem ![]() sei durch ein Paar
sei durch ein Paar
![]() , welches aus einem festen Punkt
, welches aus einem festen Punkt ![]() und einer
Basis
und einer
Basis ![]() besteht, definiert. Von diesem ausgehend wird durch die bijektive
Abbildung
besteht, definiert. Von diesem ausgehend wird durch die bijektive
Abbildung ![\begin{displaymath}
f:\left( O,X\left( x_{1},x_{2},...,x_{n}\right) \right) \; \...
...rray}{c}
x_{1}\\
x_{2}\\
\vdots \\
x_{n}
\end{array}\right] \end{displaymath}](img9.gif)
![]() kann in einem solchen Fall mit der Tangentialebene an
die Fläche in diesem Punkt identifiziert werden. Versucht man einen Vektor
kann in einem solchen Fall mit der Tangentialebene an
die Fläche in diesem Punkt identifiziert werden. Versucht man einen Vektor ![]() in der Tangentialebene in
in der Tangentialebene in ![]() , parallel in einen benachbarten Punkt
, parallel in einen benachbarten Punkt ![]() zu verschieben, so ist dies nach der euklidschen Definition von Parallelität,
aufgrund der Ortsabhängigkeit der Basisvektoren, nicht möglich. Eine 'parallelste'
Verschiebung kann jedoch auf diese Weise definiert werden, daß man
zu verschieben, so ist dies nach der euklidschen Definition von Parallelität,
aufgrund der Ortsabhängigkeit der Basisvektoren, nicht möglich. Eine 'parallelste'
Verschiebung kann jedoch auf diese Weise definiert werden, daß man ![]() räumlich parallel (im euklidschen Sinn) nach
räumlich parallel (im euklidschen Sinn) nach ![]() versetzt und diesen im
Anschluß daran in die Tangentialebene in
versetzt und diesen im
Anschluß daran in die Tangentialebene in ![]() projeziert. Diese Parallelverschiebung
gilt natürlich nur für eine differentiell kleine Entfernung zwischen
projeziert. Diese Parallelverschiebung
gilt natürlich nur für eine differentiell kleine Entfernung zwischen ![]() und
und ![]() . Es kann gezeigt werden, daß diese Art der Verschiebung, der s.g.
Parallelverschiebung eines Tensors 1. Stufe nach Levi Civita entspricht.
. Es kann gezeigt werden, daß diese Art der Verschiebung, der s.g.
Parallelverschiebung eines Tensors 1. Stufe nach Levi Civita entspricht.
![]() einer Mannigfaltigkeit heißt parallelverschoben
nach Levi Civita, entlang einer Kurve
einer Mannigfaltigkeit heißt parallelverschoben
nach Levi Civita, entlang einer Kurve
![]() mit dem Parameter
mit dem Parameter
![]() , wenn folgende Differentialgleichungen gelten
, wenn folgende Differentialgleichungen gelten![]() ) gilt die hierzu äquivalente Darstellung
) gilt die hierzu äquivalente Darstellung ![]() ,
so daß die Länge einer Kurve
,
so daß die Länge einer Kurve
![]() zwischen den Parameterwerten
zwischen den Parameterwerten
![]() und
und ![]() gegeben ist durch
gegeben ist durch ![]() entnommen werden.
entnommen werden.
![]() ) ergibt sich
nach zweifacher Integration zu
) ergibt sich
nach zweifacher Integration zu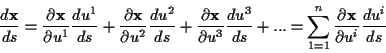
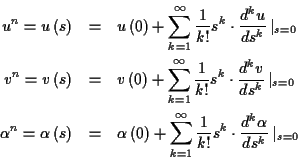
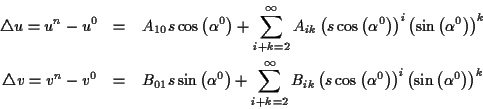
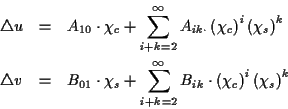
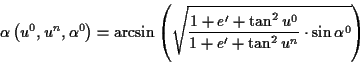
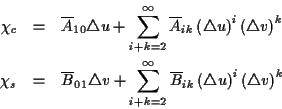
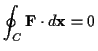
![]() , d.h. Kräfte einführt, deren Wirkungslinien
senkrecht zur einschränkenden Geometrie stehen und somit keine Arbeit verrichten.
, d.h. Kräfte einführt, deren Wirkungslinien
senkrecht zur einschränkenden Geometrie stehen und somit keine Arbeit verrichten.
![]() ist dabei so zu interpretieren,
daß sich die eingeprägte Kraft
ist dabei so zu interpretieren,
daß sich die eingeprägte Kraft
![]() mit der Trägheitskraft
mit der Trägheitskraft
![]() im Gleichgewicht befindet.
im Gleichgewicht befindet.
![]() zu sehen, bildet die Schnittgerade der schiefen
Ebene mit der
zu sehen, bildet die Schnittgerade der schiefen
Ebene mit der
![]() -Ebene den Winkel
-Ebene den Winkel ![]() mit der
mit der
![]() -Achse. Zum einen gilt daher zu jedem Zeitpunkt
-Achse. Zum einen gilt daher zu jedem Zeitpunkt
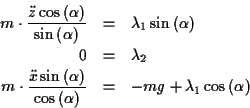
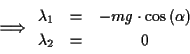
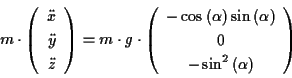
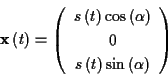
![]() eines Systems entspricht dabei der Zahl der Koordinaten, die nötig sind, um
die Ortsfunktionen der Massepunkte des Systems zu beschreiben. Über das zu wählende
Koordinatensystem kann frei verfügt werden, jedoch bestimmt die Art des Systems
die Komplexität der Lösung des Bewegungsproblems. Die Zahl der Freiheitsgrade
verringert sich nun mit der Zahl der gegebenen Nebenbedingungen. Die minimal
zur Beschreibung des Problems notwendigen Koordinaten werden als generalisierte
Koordinaten1.8
eines Systems entspricht dabei der Zahl der Koordinaten, die nötig sind, um
die Ortsfunktionen der Massepunkte des Systems zu beschreiben. Über das zu wählende
Koordinatensystem kann frei verfügt werden, jedoch bestimmt die Art des Systems
die Komplexität der Lösung des Bewegungsproblems. Die Zahl der Freiheitsgrade
verringert sich nun mit der Zahl der gegebenen Nebenbedingungen. Die minimal
zur Beschreibung des Problems notwendigen Koordinaten werden als generalisierte
Koordinaten1.8
![]() bezeichnet. Die Bewegung muß in diesen Koordinaten
zwangsfrei verlaufen. Ein System von
bezeichnet. Die Bewegung muß in diesen Koordinaten
zwangsfrei verlaufen. Ein System von ![]() Massepunkten in einem 3-D Raum
wird durch
Massepunkten in einem 3-D Raum
wird durch ![]() kartesische Koordinaten
kartesische Koordinaten
![]() für
für ![]() und
und ![]() beschrieben. Sei
beschrieben. Sei ![]() die Zahl der
Randbedingungen, so ergibt sich die Zahl der Freiheitsgrade des Systems nach
die Zahl der
Randbedingungen, so ergibt sich die Zahl der Freiheitsgrade des Systems nach
![]() . Hieraus folgt, daß im Falle
. Hieraus folgt, daß im Falle ![]() die Bewegung des Punktsystems
durch die Bedingungsgleichungen eindeutig bestimmt ist.
die Bewegung des Punktsystems
durch die Bedingungsgleichungen eindeutig bestimmt ist.
![]() läßt sich wie folgt darstellen
läßt sich wie folgt darstellen 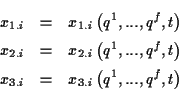
![]() bezüglich des rechtwinklig kartesischen
Sytems ist gegeben durch
bezüglich des rechtwinklig kartesischen
Sytems ist gegeben durch ![\begin{displaymath}
\mathbf{x}_{.i}=\left[ \begin{array}{c}
x^{1}_{.i}\\
x^{2}_...
...{.i}
\end{array}\right] =x^{j}_{.i}\mathbf{e}_{j}\; ,\; j=1,2,3\end{displaymath}](img281.gif)
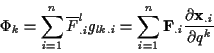
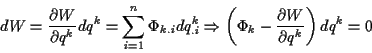
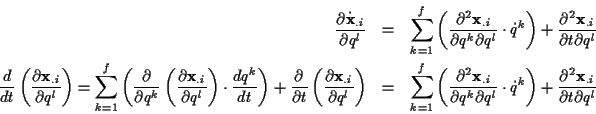
![]() ) in generalisierten
Koordinaten lautet
) in generalisierten
Koordinaten lautet 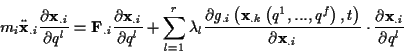
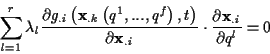
![]() ) an so gilt
allgemein
) an so gilt
allgemein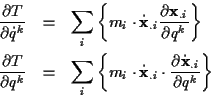
![]() und
und ![]() so, daß das s.g. Wirkungsintegral
so, daß das s.g. Wirkungsintegral![]() dargelegt.
dargelegt.
![]() ersichtlich, kann im vorliegenden kartesischen
Koordinatensystem
ersichtlich, kann im vorliegenden kartesischen
Koordinatensystem
![]() eine generalisierte Koordinate
eine generalisierte Koordinate ![]() eingeführt werden, die die Bewegung
des Körpers ausreichend beschreibt. In diesem Fall ist leicht erkennbar, daß
das System nur einen Freiheitsgrad besitzt und somit eine generalisierte
Koordinate zur Beschreibung der Bewegung ausreicht. Die Koordinate
eingeführt werden, die die Bewegung
des Körpers ausreichend beschreibt. In diesem Fall ist leicht erkennbar, daß
das System nur einen Freiheitsgrad besitzt und somit eine generalisierte
Koordinate zur Beschreibung der Bewegung ausreicht. Die Koordinate ![]() unterliegt keinerlei Zwängen, d.h. sie kann je nach Wahl der Anfangsbedingungen
jeden Wert annehmen. Die Transformationsgleichungen lauten in diesem Fall
unterliegt keinerlei Zwängen, d.h. sie kann je nach Wahl der Anfangsbedingungen
jeden Wert annehmen. Die Transformationsgleichungen lauten in diesem Fall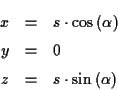
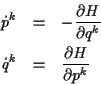
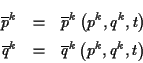
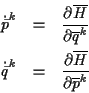
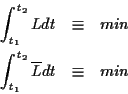
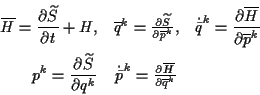
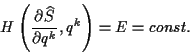
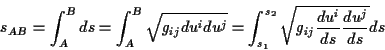
![]() )
und wenn das Potential den Wert
)
und wenn das Potential den Wert ![]() erhält, daß die Gesamtenergie, die
in einem solchen Fall durch die Hamiltonfunktion
erhält, daß die Gesamtenergie, die
in einem solchen Fall durch die Hamiltonfunktion ![]() gegeben ist, nur aus
dem Anteil der kinetischen Energie besteht. Wichtig ist hierbei die Betrachtung
des kinematischen Linienelementes
gegeben ist, nur aus
dem Anteil der kinetischen Energie besteht. Wichtig ist hierbei die Betrachtung
des kinematischen Linienelementes
![]() , welches beim Lagrangeformalismus
das geometrische Linienelement ersetzt. Falls nun der Hamiltonformalismus angewandt
werden soll, so muß die quadratische Form für die kinetische Energie durch die
Metrik des Rotationsellipsoides ersetzt werden. Demzufolge ergibt sich analog
zu (
, welches beim Lagrangeformalismus
das geometrische Linienelement ersetzt. Falls nun der Hamiltonformalismus angewandt
werden soll, so muß die quadratische Form für die kinetische Energie durch die
Metrik des Rotationsellipsoides ersetzt werden. Demzufolge ergibt sich analog
zu (![]() ) für die Hamiltonfunktion
) für die Hamiltonfunktion![]() )
und
)
und ![\begin{displaymath}
\left[ \widetilde{g}_{ij}\left( u^{\alpha }\right) \right] =...
...
0 & N^{2}\cos ^{2}\left( \varphi \right)
\end{array}\right] \end{displaymath}](img410.gif)
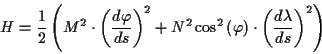
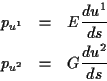
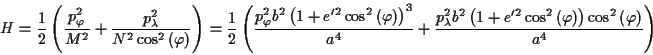
![]() mit
mit
![]() aus, was an (
aus, was an (![]() ) nichts ändert. Der Metriktensor
hat dann die etwas einfachere Form
) nichts ändert. Der Metriktensor
hat dann die etwas einfachere Form![]() in Abhängigkeit der von reduzierten Breite
in Abhängigkeit der von reduzierten Breite ![]() .
.
![]() ,
die Werte
,
die Werte ![]() sowie
sowie ![]() seien als bekannt vorausgesetzt.
Das Problem besteht nun darin, den Funktionswert der Funktion
seien als bekannt vorausgesetzt.
Das Problem besteht nun darin, den Funktionswert der Funktion
![]() an der Stelle
an der Stelle ![]() zu bestimmen. Im weiteren sei dieser mit
zu bestimmen. Im weiteren sei dieser mit ![]() bezeichnet. Die zugehörige Integralgleichung lautet damit
bezeichnet. Die zugehörige Integralgleichung lautet damit ![]() an der Stelle
an der Stelle ![]() in eine Taylorreihe
in eine Taylorreihe ![]() ,
, ![]() ,
, ![]() der Funktion
der Funktion
![]() an den Stellen
an den Stellen ![]() ,
,
![]() und
und ![]() vorliegen.
Mit diesen Werten folgt mit der Prismaregel2.1 :
vorliegen.
Mit diesen Werten folgt mit der Prismaregel2.1 : ![]() , kann das
Verfahren abgeändert werden. Die Abbildung
, kann das
Verfahren abgeändert werden. Die Abbildung ![]() gibt das Prinzip des
Verfahrens nach Runge wieder.
gibt das Prinzip des
Verfahrens nach Runge wieder.
![]() , wobei sich
, wobei sich ![]() als eine Funktion der Integrationsweite
als eine Funktion der Integrationsweite
![]() und einer diskreten Näherungsfunktion, die im weiteren mit
und einer diskreten Näherungsfunktion, die im weiteren mit ![]() bezeichnet wird, darstellen läßt . Für
bezeichnet wird, darstellen läßt . Für ![]() 2.2 gilt:
2.2 gilt: 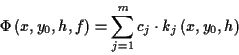
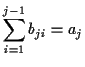 und
und
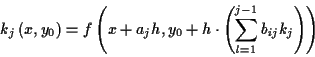
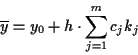
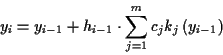
![]() eine Matrix ansetzt, in der für jede Gleichung
des Systems eine Spalte sukzessive in den Iterationsschritten bestimmt wird.
eine Matrix ansetzt, in der für jede Gleichung
des Systems eine Spalte sukzessive in den Iterationsschritten bestimmt wird.
![]() zeigt ein Flußdiagramm) von der MATLAB Eingabeaufforderung geschieht über:
zeigt ein Flußdiagramm) von der MATLAB Eingabeaufforderung geschieht über:
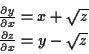
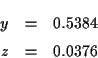
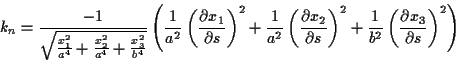
![]() , die Variablen mit
, die Variablen mit ![]() bezeichnet.
bezeichnet.
![]() stehen hierbei für die kartesischen Koordinaten des Anfangspunktes,
die drei übrigen Variablen bezeichnen die Komponenten des Tangenteneinheitsvektors
im Anfangspunkt, die zunächst über die gegebenen Größen zu berechnen sind. Wie
bereits erwähnt, besitzt die implizite Art der Flächendarstellung und damit
das aus dieser abgeleitete Differentialgleichungssystem, den Vorteil, daß es
frei von Singularitäten ist. Den meisten Verfahren, die bei der numerischen
Integration der ersten Hauptaufgabe Verwendung finden, liegt das, in der Literatur
meist angegebene, Gleichungssystem
stehen hierbei für die kartesischen Koordinaten des Anfangspunktes,
die drei übrigen Variablen bezeichnen die Komponenten des Tangenteneinheitsvektors
im Anfangspunkt, die zunächst über die gegebenen Größen zu berechnen sind. Wie
bereits erwähnt, besitzt die implizite Art der Flächendarstellung und damit
das aus dieser abgeleitete Differentialgleichungssystem, den Vorteil, daß es
frei von Singularitäten ist. Den meisten Verfahren, die bei der numerischen
Integration der ersten Hauptaufgabe Verwendung finden, liegt das, in der Literatur
meist angegebene, Gleichungssystem ![\begin{displaymath}
\left[ g_{ij}\right] =\left[ \begin{array}{cc}
M^{2} & 0\\
0 & N^{2}\cos ^{2}\left( \varphi \right)
\end{array}\right] \end{displaymath}](img508.gif)
![]() )
über eine Anfangswertaufgabe auf die zuvor eingeführte Funktion RK7multi
zurückgegriffen. Der Funktionsaufruf lautet in diesem Fall:
)
über eine Anfangswertaufgabe auf die zuvor eingeführte Funktion RK7multi
zurückgegriffen. Der Funktionsaufruf lautet in diesem Fall:
![]() Iterationen von denen der
Lösung mit
Iterationen von denen der
Lösung mit ![]() Iterationen nur noch um eine vorgegebene Schranke
Iterationen nur noch um eine vorgegebene Schranke ![]() unterscheiden. Setzt man beispielsweise als Schranke für die Genauigkeit der
kartesischen Koordinaten der Endpunkte einen Wert von
unterscheiden. Setzt man beispielsweise als Schranke für die Genauigkeit der
kartesischen Koordinaten der Endpunkte einen Wert von
![]() an, so ergibt der in Abb.
an, so ergibt der in Abb. ![]() dargestellte, wie zu erwarten
lineare, Zusammenhang zwischen der Anzahl der benötigten Iterationen und der
Länge der geodätischen Linie.
dargestellte, wie zu erwarten
lineare, Zusammenhang zwischen der Anzahl der benötigten Iterationen und der
Länge der geodätischen Linie.
![]() , Abplattung
, Abplattung ![]() und geforderte Genauigkeit
und geforderte Genauigkeit ![]() in einer Funktion
in einer Funktion
![]() zusammenzufassen.
Es bietet sich dabei an, die Einflüsse von
zusammenzufassen.
Es bietet sich dabei an, die Einflüsse von ![]() und
und ![]() auf den in Abb.
auf den in Abb. ![]() dargestellten linearen Zusammenhang
dargestellten linearen Zusammenhang
![]() zu untersuchen. Im ersten Graphen von Abb.
zu untersuchen. Im ersten Graphen von Abb. ![]() sind zunächst verschiedene
sind zunächst verschiedene
![]() Kurven für unterschiedliche
Abplattungswerte
Kurven für unterschiedliche
Abplattungswerte ![]() in
in
![]() dargestellt. Darunter
folgt derselbe Graph für variierende
dargestellt. Darunter
folgt derselbe Graph für variierende ![]() (
(
![]() ). Aus diesen beiden Abbildungen folgt, daß die Einflüsse der anderen beiden
Parameter auf
). Aus diesen beiden Abbildungen folgt, daß die Einflüsse der anderen beiden
Parameter auf
![]() nichts an deren linearer Eigenschaft
ändern. Im weiteren sind daher die Veränderungen der Parameter
nichts an deren linearer Eigenschaft
ändern. Im weiteren sind daher die Veränderungen der Parameter
![]() und
und
![]() des Polynoms erster Ordnung
des Polynoms erster Ordnung
![]() bei Änderung von
bei Änderung von ![]() und
und ![]() zu untersuchen. Für
die Abhängigkeit der Steigung
zu untersuchen. Für
die Abhängigkeit der Steigung
![]() der Geraden
der Geraden
![]() von der geforderten Genauigkeit
von der geforderten Genauigkeit ![]() (vgl. Abb.
(vgl. Abb. ![]() ),
ergibt sich, nach Ermittlung der
),
ergibt sich, nach Ermittlung der
![]() über lineare
Regression, der folgende logarithmische Zusammenhang :
über lineare
Regression, der folgende logarithmische Zusammenhang : ![]() läßt sich durch
ein Polynom dritten Grades in
läßt sich durch
ein Polynom dritten Grades in ![]() approximieren:
approximieren: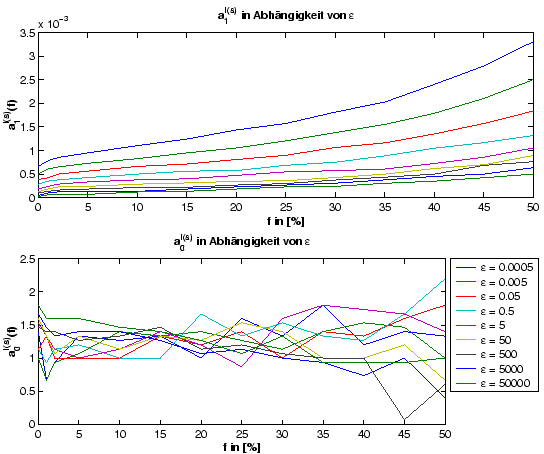
![]() zeigt eine graphische Darstellung der
zeigt eine graphische Darstellung der
![]() aus Tabelle
aus Tabelle ![]() .
Wie man dieser entnehmen kann, lohnt es aufgrund der Sprünge nicht, die sich
ergebenden Zusammenhänge funktional zu approximieren.
.
Wie man dieser entnehmen kann, lohnt es aufgrund der Sprünge nicht, die sich
ergebenden Zusammenhänge funktional zu approximieren.
![]() die
zugehörigen Polynomkoeffizienten bestimmt, dann der Funktionswert dieses Polynoms
an der Stelle der gegebenen Abplattung ermittelt und mit diesem die Funktion
die
zugehörigen Polynomkoeffizienten bestimmt, dann der Funktionswert dieses Polynoms
an der Stelle der gegebenen Abplattung ermittelt und mit diesem die Funktion
![]() ausgewertet wird. Wie aus Abb.
ausgewertet wird. Wie aus Abb. ![]() unten ersichtlich, ist es angebracht den y-Achsenabschnitt, der scheinbar keinem
funktionalen Zusammenhang folgt ,als Konstante mit dem Wert
unten ersichtlich, ist es angebracht den y-Achsenabschnitt, der scheinbar keinem
funktionalen Zusammenhang folgt ,als Konstante mit dem Wert ![]() einzuführen.
Damit ergibt sich folgende Iterationsfunktion:
einzuführen.
Damit ergibt sich folgende Iterationsfunktion:![]() sind nun die Ergebnisse des RKF72.10 zum Vergleich in der letzten Spalte angeordnet. Bei der Berechnung über
geod_haupt_1.m wurde zunächst die Zahl der Iterationen auf 35 festgelegt.
Die Werte in den Klammern enthalten im Vergleich hierzu die Änderungen, die
sich nach Vorgabe einer Genauigkeit von
sind nun die Ergebnisse des RKF72.10 zum Vergleich in der letzten Spalte angeordnet. Bei der Berechnung über
geod_haupt_1.m wurde zunächst die Zahl der Iterationen auf 35 festgelegt.
Die Werte in den Klammern enthalten im Vergleich hierzu die Änderungen, die
sich nach Vorgabe einer Genauigkeit von
![]() über die Auswertung der empirischen Iterationsfunktion zeigten. Die Zahl der
sich für diese Genauigkeit nach (
über die Auswertung der empirischen Iterationsfunktion zeigten. Die Zahl der
sich für diese Genauigkeit nach (![]() ) ergebenden nötigen
Iterationen ist zusätzlich angegeben. Der Tabelle kann entnommen werden, daß
die Ergebnisse für die Koordinaten sich bei Längen bis zu
) ergebenden nötigen
Iterationen ist zusätzlich angegeben. Der Tabelle kann entnommen werden, daß
die Ergebnisse für die Koordinaten sich bei Längen bis zu ![]() nicht
unterscheiden. Werden die Entfernungen jedoch größer treten hier Abweichungen
im Bereich einiger zehntel Millimeter auf. Der Azimut im Endpunkt wird nur für
nicht
unterscheiden. Werden die Entfernungen jedoch größer treten hier Abweichungen
im Bereich einiger zehntel Millimeter auf. Der Azimut im Endpunkt wird nur für
![]() identisch erhalten. Für
identisch erhalten. Für ![]() treten Abweichungen
im Bereich von
treten Abweichungen
im Bereich von ![]() Sekunden auf. Da Abweichungen in dieser Größenordnung
auch bei Aringers Vergleich der verschiedenen Integratoren vorkommen2.11, ist es schwierig auf deren Ursache zu schließen. Ein möglicher Grund könnte
in der unterschiedlichen Größenordnung der Anfangswerte liegen, die jedoch durch
eine Änderung der Skalierung umgangen werden kann.
Sekunden auf. Da Abweichungen in dieser Größenordnung
auch bei Aringers Vergleich der verschiedenen Integratoren vorkommen2.11, ist es schwierig auf deren Ursache zu schließen. Ein möglicher Grund könnte
in der unterschiedlichen Größenordnung der Anfangswerte liegen, die jedoch durch
eine Änderung der Skalierung umgangen werden kann.
![]() ) so trifft dies hier ebenfalls zu. Die gesuchte Entfernung
) so trifft dies hier ebenfalls zu. Die gesuchte Entfernung
![]() tritt als Integrationsvariable auf. Eine Möglichkeit der Lösung dieses
Problems besteht darin, ein anderes gleichwertiges System aufzustellen, in dem
das Integrationsintervall einer neu einzuführenden unabhängigen Variablen gegeben
ist. ARINGER stellt ein solches System für die Differentialgleichung der geodätischen
Linie in kartesischen Koordinaten in seiner Dissertation2.12 vor.
tritt als Integrationsvariable auf. Eine Möglichkeit der Lösung dieses
Problems besteht darin, ein anderes gleichwertiges System aufzustellen, in dem
das Integrationsintervall einer neu einzuführenden unabhängigen Variablen gegeben
ist. ARINGER stellt ein solches System für die Differentialgleichung der geodätischen
Linie in kartesischen Koordinaten in seiner Dissertation2.12 vor.
![]() aufgestellt. Hierbei bezeichne
aufgestellt. Hierbei bezeichne
![]() die Lösung der Anfangswertaufgabe mit dem Näherungsvektor
die Lösung der Anfangswertaufgabe mit dem Näherungsvektor
![]() in der
in der ![]() Iteration und
Iteration und
![]() die vorgegebenen
Randwerte für das RWP (geg. Endpunktkoordinaten). Im Falle der zweiten geodätischen
Hauptaufgabe ergeben sich die folgenden Randbedingungen:
die vorgegebenen
Randwerte für das RWP (geg. Endpunktkoordinaten). Im Falle der zweiten geodätischen
Hauptaufgabe ergeben sich die folgenden Randbedingungen:
![\( \mathbf{y}_{a}=\left[ \begin{array}{c}
x\\
y\\
z\\
t_{1}\\
t_{2}\\
t_{3}
\end{array}\right] \)](img582.gif) und
und
![\( \widehat{\mathbf{y}}=\left[ \begin{array}{c}
\widehat{x}\\
\widehat{y}\\
\widehat{z}
\end{array}\right] \)](img583.gif)
![]() ) eine nichtlineare Gleichung in
) eine nichtlineare Gleichung in
![]() ,
die mit Hilfe des allgemeinen Newtonverfahrens2.14 iterativ gelöst werden kann. Die Bestimmung der Näherungswerte für die
,
die mit Hilfe des allgemeinen Newtonverfahrens2.14 iterativ gelöst werden kann. Die Bestimmung der Näherungswerte für die ![]() te Iteration erfolgt über:
te Iteration erfolgt über:
![]() ) nicht explizit durchgeführt
werden kann, muß an dieser Stelle der Differentialquotient durch den Differenzenquotienten
ersetzt werden.
) nicht explizit durchgeführt
werden kann, muß an dieser Stelle der Differentialquotient durch den Differenzenquotienten
ersetzt werden.
![]() , welcher durch eine geeignete Näherung
zu ermitteln ist, wird die
, welcher durch eine geeignete Näherung
zu ermitteln ist, wird die ![]() -te Komponente um einen noch festzulegenden
Wert
-te Komponente um einen noch festzulegenden
Wert
![]() variiert und erneut eine Anfangswertaufgabe
berechnet. Nach der Iteration über
variiert und erneut eine Anfangswertaufgabe
berechnet. Nach der Iteration über ![]() erhält man damit ein lineares Gleichungssystem
für die Ermittlung des Vektors der Verbesserungen
erhält man damit ein lineares Gleichungssystem
für die Ermittlung des Vektors der Verbesserungen
![]() . Die
Startwerte für den
. Die
Startwerte für den ![]() 'ten Schritt erhält man über (
'ten Schritt erhält man über (![]() ).
Nach einer erneuten Berechnung des AWP's kann ein Abbruchkriterium ()
derart eingefügt werden, daß falls die euklidsche Distanz des berechneten Endpunktes
vom Sollwert eine Schranke
).
Nach einer erneuten Berechnung des AWP's kann ein Abbruchkriterium ()
derart eingefügt werden, daß falls die euklidsche Distanz des berechneten Endpunktes
vom Sollwert eine Schranke ![]() unterschreitet, das Schießverfahren
beendet wird. Die Abb.
unterschreitet, das Schießverfahren
beendet wird. Die Abb. ![]() zeigt das Prinzip des Schießverfahrens
am Beispiel der 2. geodätischen Hauptaufgabe. Es sind im weiteren noch geeignete
Näherungswerte für den Startvektor
zeigt das Prinzip des Schießverfahrens
am Beispiel der 2. geodätischen Hauptaufgabe. Es sind im weiteren noch geeignete
Näherungswerte für den Startvektor
![]() und die Wahl der
Größenordnung der Variationen der Näherungsvektoren sowie deren Änderungen in
der Iterationsphase zu bestimmen. Bei den Größenordnungen der Variationen handelt
es sich um empirisch abzuleitende Werte, auf die im Hinblick auf den Umfang
der Arbeit, hier nicht weiter eingegangen werden soll.
und die Wahl der
Größenordnung der Variationen der Näherungsvektoren sowie deren Änderungen in
der Iterationsphase zu bestimmen. Bei den Größenordnungen der Variationen handelt
es sich um empirisch abzuleitende Werte, auf die im Hinblick auf den Umfang
der Arbeit, hier nicht weiter eingegangen werden soll.
![]() der Fläche im Anfangspunkt A bestimmt werden.
Mit der Normierung
der Fläche im Anfangspunkt A bestimmt werden.
Mit der Normierung 
![\begin{displaymath}
\mathbf{n}_{a}=\rho _{a}\left[ \begin{array}{c}
\frac{x_{a}}...
...
\frac{y_{a}}{a^{2}}\\
\frac{z_{a}}{b^{2}}
\end{array}\right] \end{displaymath}](img597.gif)
![\begin{displaymath}
p_{\perp }=\left[ \begin{array}{c}
x_{b}-x_{a}\\
y_{b}-y_{a}\\
z_{b}-z_{a}
\end{array}\right] ^{T}\cdot \mathbf{n}_{a}\end{displaymath}](img599.gif)
![]() bestimmt und über den Kosinussatz der sphärischen Geometrie, unter Betrachtung
der ellipsoidischen Koordinaten als Kugelkoordinaten, sowie der Annahme
bestimmt und über den Kosinussatz der sphärischen Geometrie, unter Betrachtung
der ellipsoidischen Koordinaten als Kugelkoordinaten, sowie der Annahme
![]() ,
ein Näherungswert für die Länge der geodätischen Linie ermittelt. Es zeigt sich,
daß diese Näherung jedoch, aufgrund der lokalen Konvergenz des Schießverfahrens,
nur ausreichend ist für Strecken bis 5000km, so daß im weiteren die Länge eines
Vertikalschnittes als Näherung Verwendung findet. Die Vertikalschnittebene wird
von
,
ein Näherungswert für die Länge der geodätischen Linie ermittelt. Es zeigt sich,
daß diese Näherung jedoch, aufgrund der lokalen Konvergenz des Schießverfahrens,
nur ausreichend ist für Strecken bis 5000km, so daß im weiteren die Länge eines
Vertikalschnittes als Näherung Verwendung findet. Die Vertikalschnittebene wird
von
![]() und
und
![]() in A aufgespannt. Um die
Berechnung zu vereinfachen reicht es aus, das Problem in einem 2-D Koordinatensystem,
in dem sich der Vertikalschnitt als ebene Kurve eindeutig darstellen läßt, zu
betrachten. Ohne näher auf die Transformation einzugehen, sei erwähnt, daß der
Ursprung des Koordinatensystems in den Anfangspunkt A verschoben wurde, die
neue x-Achse in Richtung
in A aufgespannt. Um die
Berechnung zu vereinfachen reicht es aus, das Problem in einem 2-D Koordinatensystem,
in dem sich der Vertikalschnitt als ebene Kurve eindeutig darstellen läßt, zu
betrachten. Ohne näher auf die Transformation einzugehen, sei erwähnt, daß der
Ursprung des Koordinatensystems in den Anfangspunkt A verschoben wurde, die
neue x-Achse in Richtung
![]() und die neue z-Achse in Richtung
und die neue z-Achse in Richtung
![]() weist. (vgl. hierzu Abb.
weist. (vgl. hierzu Abb. ![]() ) Es
ergibt sich die folgende Gleichung für die Vertikalschnittkurve aus der Gleichung
des Ellipsoides im gedrehten ebenen System:
) Es
ergibt sich die folgende Gleichung für die Vertikalschnittkurve aus der Gleichung
des Ellipsoides im gedrehten ebenen System:
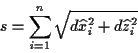
![]() zeigt, daß es numerisch sinnvoll ist,
das gesamte Integrationsintervall in 3 Teilintervalle zu ordnen. Im ersten,
sowie im dritten wird
zeigt, daß es numerisch sinnvoll ist,
das gesamte Integrationsintervall in 3 Teilintervalle zu ordnen. Im ersten,
sowie im dritten wird ![]() , im zweiten
, im zweiten ![]() als
unabhängige Variable gewählt. Damit findet bei der Berechnung der Koordinatendifferentiale
im zweiten Intervall Gleichung (
als
unabhängige Variable gewählt. Damit findet bei der Berechnung der Koordinatendifferentiale
im zweiten Intervall Gleichung (![]() ), in den übrigen
Gleichung (
), in den übrigen
Gleichung (![]() ) Verwendung. Im ersten Intervall erhält
(
) Verwendung. Im ersten Intervall erhält
(![]() ) das Vorzeichen ``+'', im dritten ``-``.
Die Genauigkeit der Berechnung ist abhängig von der Zahl
) das Vorzeichen ``+'', im dritten ``-``.
Die Genauigkeit der Berechnung ist abhängig von der Zahl ![]() der Teilintervalle
der Teilintervalle
![]() bzw.
bzw.
![]() .
.
![]() und
und ![]() gegebenem Ellipsoid, kann die 2. geodätische Hauptaufgabe
nach dem Schießverfahren gelöst werden2.15.
gegebenem Ellipsoid, kann die 2. geodätische Hauptaufgabe
nach dem Schießverfahren gelöst werden2.15.
![]() )
enthält Eingabefelder für
)
enthält Eingabefelder für
![]() ermittelt.
ermittelt.
![]() werden die Ergebnisse, wie auch schon
bei der ersten Hauptaufgabe, Aringers Daten gegenübergestellt. Die der Berechnung
zugrundeliegenden Ellipsoidparameter waren
werden die Ergebnisse, wie auch schon
bei der ersten Hauptaufgabe, Aringers Daten gegenübergestellt. Die der Berechnung
zugrundeliegenden Ellipsoidparameter waren![]() Sekunden. Die Entfernung wird im Gegensatz dazu
identisch erhalten. Es verwundert, daß Aringer bei den Beispielen 2 - 6 das
Azimut auf die 7-te Nachkommastelle genau betimmen kann (vgl. Beispiele für
die 1. geodätische Hauptaufgabe), obwohl er die Koordinaten des Endpunktes,
die er aus der Berechnung der Anfangswertaufgaben ermittelt hat, nur mit 3 Nachkommastellen
ansetzt. Das führt dazu, daß der Vergleich der Ergebnisse nicht besonders aussagekräftig
ist.
Sekunden. Die Entfernung wird im Gegensatz dazu
identisch erhalten. Es verwundert, daß Aringer bei den Beispielen 2 - 6 das
Azimut auf die 7-te Nachkommastelle genau betimmen kann (vgl. Beispiele für
die 1. geodätische Hauptaufgabe), obwohl er die Koordinaten des Endpunktes,
die er aus der Berechnung der Anfangswertaufgaben ermittelt hat, nur mit 3 Nachkommastellen
ansetzt. Das führt dazu, daß der Vergleich der Ergebnisse nicht besonders aussagekräftig
ist.
![]() . Hier wird zum einen die gewünschte
Zahl der Stützpunkte2.21 der geodätischen Linie eingetragen, zum anderen besteht die Möglichkeit zwischen
zwei Arten der Darstellung des Ellipsoides zu wählen. In der Gitterdarstellung
werden nur die, über eine Hilfsfunktion berechneten Stützpunkte eines geographischen
ellipsoidischen Koordinatensystems mit Linien verbunden, dargestellt. Über die
Zahl der Stützstellen läßt sich frei verfügen. Bei der Flächendarstellung hingegen
werden diese Gitterelemente farbig ausgefüllt, was dazu führt, daß die später
zwischen die Stützpunkte gezeichneten Verbindungslinien nicht mehr komplett
sichtbar sind.
. Hier wird zum einen die gewünschte
Zahl der Stützpunkte2.21 der geodätischen Linie eingetragen, zum anderen besteht die Möglichkeit zwischen
zwei Arten der Darstellung des Ellipsoides zu wählen. In der Gitterdarstellung
werden nur die, über eine Hilfsfunktion berechneten Stützpunkte eines geographischen
ellipsoidischen Koordinatensystems mit Linien verbunden, dargestellt. Über die
Zahl der Stützstellen läßt sich frei verfügen. Bei der Flächendarstellung hingegen
werden diese Gitterelemente farbig ausgefüllt, was dazu führt, daß die später
zwischen die Stützpunkte gezeichneten Verbindungslinien nicht mehr komplett
sichtbar sind.
![]() zeigt das graphische Ergebnis einer Ephemeridenberechnung
mit 20 Stützstellen bei einer Länge der geodätischen Linie von 15000km.
zeigt das graphische Ergebnis einer Ephemeridenberechnung
mit 20 Stützstellen bei einer Länge der geodätischen Linie von 15000km.
![]() -
-![]() kurz aufgeführt.
kurz aufgeführt.
![]() und
und ![]() werden in diesem Zusammenhang als die ellipsoidischen
Parallelkoordinaten des Punktes
werden in diesem Zusammenhang als die ellipsoidischen
Parallelkoordinaten des Punktes ![]() bezeichnet. Sie lassen sich als Gaußsche
Flächenparameter auf dem Ellipsoid interpretieren. Die als Ordinatenlinien bezeichneten
geodätischen Linien verlaufen auf dem Ellipsoid weder eben noch sind es geschlossene
Kurven. Ebenso bilden die Abzissenlinien oder geodätische Parallelen, zwar geschlossene,
jedoch keine ebenen Kurven. An Stelle des Querpols, der sich bei Einführung
eines Parallelkoordinatensystems als Schnittpunkt der Geodäten auf der Kugel
ergibt, bildet sich im Falle eines Rotationsellipsoides ein, zum Äquator symmetrisches
Gebiet, das durch eine asteroidenförmige Flächenkurve begrenzt wird. Mit Hilfe
des im folgenden beschriebenen Programms läßt sich diese Figur anhand eines
dreidimensionalen Gittermodells des Koordinatennetzes in Abhängigkeit gewisser
Parameter graphisch darstellen.
bezeichnet. Sie lassen sich als Gaußsche
Flächenparameter auf dem Ellipsoid interpretieren. Die als Ordinatenlinien bezeichneten
geodätischen Linien verlaufen auf dem Ellipsoid weder eben noch sind es geschlossene
Kurven. Ebenso bilden die Abzissenlinien oder geodätische Parallelen, zwar geschlossene,
jedoch keine ebenen Kurven. An Stelle des Querpols, der sich bei Einführung
eines Parallelkoordinatensystems als Schnittpunkt der Geodäten auf der Kugel
ergibt, bildet sich im Falle eines Rotationsellipsoides ein, zum Äquator symmetrisches
Gebiet, das durch eine asteroidenförmige Flächenkurve begrenzt wird. Mit Hilfe
des im folgenden beschriebenen Programms läßt sich diese Figur anhand eines
dreidimensionalen Gittermodells des Koordinatennetzes in Abhängigkeit gewisser
Parameter graphisch darstellen.
![\begin{displaymath}
\mathbf{x}=\left[ \begin{array}{c}
6378388\; m\\
0\; m\\
0\; m
\end{array}\right] \end{displaymath}](img716.gif)
![]() bezeichnet wurden, beigefügt. Zur Programmierung der
Oberfläche kann leider kein Quellcode abgegeben werden, da diese interaktiv,
per Drag & Drop, geschieht und hierbei zusätzlich entstehender Code in binären
Dateien abgespeichert wird. Als Beispiel für ein, bei der Oberflächenprogrammierung
automatisch von MATLAB erstelltes Script, kann der Ausdruck der Datei liniendarstellung.m,
welche den Aufbau der Oberfläche aus Abb.
bezeichnet wurden, beigefügt. Zur Programmierung der
Oberfläche kann leider kein Quellcode abgegeben werden, da diese interaktiv,
per Drag & Drop, geschieht und hierbei zusätzlich entstehender Code in binären
Dateien abgespeichert wird. Als Beispiel für ein, bei der Oberflächenprogrammierung
automatisch von MATLAB erstelltes Script, kann der Ausdruck der Datei liniendarstellung.m,
welche den Aufbau der Oberfläche aus Abb. ![]() regelt, ebenfalls
dem Anhang entnommen werden.
regelt, ebenfalls
dem Anhang entnommen werden.